
【题目】在矩形ABCD中,AB=5,BC=12,点A在⊙B上,如果⊙D与⊙B相交,且点B在⊙D内,那么⊙D的半径长可以等于________.(只需写出一个符合要求的数)
 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:初中数学 来源: 题型:
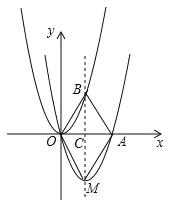
【题目】如图,在平面直角坐标系中,抛物线y1=ax(x﹣2)与x轴交于O、A两点,顶点为M,对称轴BM交抛物线![]() 于点B,交x轴于点C,连接OB、AB、OM、AM,已知0<a<4,四边形OMAB的面积为S.
于点B,交x轴于点C,连接OB、AB、OM、AM,已知0<a<4,四边形OMAB的面积为S.
特例探究:填表:

归纳证明:
当a=2时,证明四边形OMAB是菱形;
拓展应用
(1)将抛物线y1=ax(x﹣2)改为抛物线y3=ax(x﹣2m)(m>0),其他条件不变,当四边形OMAB为正方形时,a= ,m= .
(2)将抛物线y1=ax(x﹣2)改为抛物线y3=ax(x﹣2m)(m>0),其他条件不变,S= (用含m的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=﹣x+3与抛物线![]() 交于A、B两点,点A在x轴上,点B的横坐标为
交于A、B两点,点A在x轴上,点B的横坐标为![]() .动点P在抛物线上运动(不与点A、B重合),过点P作y轴的平行线,交直线AB于点Q.当PQ不与y轴重合时,以PQ为边作正方形PQMN,使MN与y轴在PQ的同侧,连结PM.设点P的横坐标为m.
.动点P在抛物线上运动(不与点A、B重合),过点P作y轴的平行线,交直线AB于点Q.当PQ不与y轴重合时,以PQ为边作正方形PQMN,使MN与y轴在PQ的同侧,连结PM.设点P的横坐标为m.
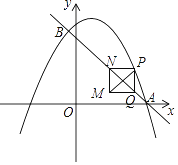
(1)求b、c的值.
(2)当点N落在直线AB上时,直接写出m的取值范围.
(3)当点P在A、B两点之间的抛物线上运动时,设正方形PQMN的周长为C,求C与m之间的函数关系式,并写出C随m增大而增大时m的取值范围.
(4)当△PQM与坐标轴有2个公共点时,直接写出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
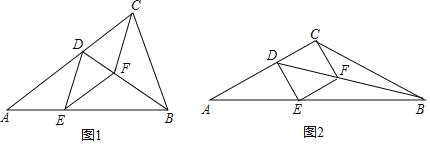
【题目】已知BD是△ABC的角平分线,点E在边AB上,BC=BE,过点E作EF∥AC,交BD于点F,连接CF.
(1)如图1,求证:四边形CDEF是菱形;
(2)如图2,当四边形CDEF是正方形,且AC=BC时,在不添加辅助线的情况下,请直接写出图中度数等于30°的角.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(9分)已知:![]() ABCD的两边AB,AD的长是关于x的方程
ABCD的两边AB,AD的长是关于x的方程![]() 的两个实数根.
的两个实数根.
(1)当m为何值时,四边形ABCD是菱形?求出这时菱形的边长;
(2)若AB的长为2,那么![]() ABCD的周长是多少?
ABCD的周长是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线![]() (其中
(其中![]() 为常数,
为常数,![]() ),
),![]() 取不同数值时,可得不同直线,请研究这些直线的共同特征.
取不同数值时,可得不同直线,请研究这些直线的共同特征.
实践操作
(1)当![]() 时,直线
时,直线![]() 的解析式为________,请在图1中画出图象.
的解析式为________,请在图1中画出图象.
当![]() 时,直线
时,直线![]() 的解析式为________,请在图2中画出图象
的解析式为________,请在图2中画出图象
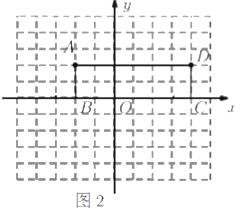
(2)探索发现:
直线![]() 必经过点(_______,_______).
必经过点(_______,_______).
(3)类比迁移:
矩形![]() 如图2所示,若直线
如图2所示,若直线![]() 分矩形
分矩形![]() 的面积为相等的两部分,请在图中直接画出这条直线.
的面积为相等的两部分,请在图中直接画出这条直线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了“创建文明城市,建设美丽家园”,我市某社区将辖区内的一块面积为1000m2的空地进行绿化,一部分种草,剩余部分栽花,设种草部分的面积为![]() (m2),种草所需费用
(m2),种草所需费用![]() 1(元)与
1(元)与![]() (m2)的函数关系式为
(m2)的函数关系式为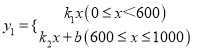 ,其图象如图所示:栽花所需费用
,其图象如图所示:栽花所需费用![]() 2(元)与x(m2)的函数关系式为
2(元)与x(m2)的函数关系式为![]() 2=﹣0.01
2=﹣0.01![]() 2﹣20
2﹣20![]() +30000(0≤
+30000(0≤![]() ≤1000).
≤1000).
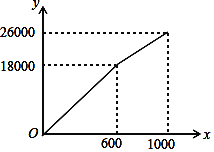
(1)请直接写出k1、k2和b的值;
(2)设这块1000m2空地的绿化总费用为W(元),请利用W与![]() 的函数关系式,求出绿化总费用W的最大值;
的函数关系式,求出绿化总费用W的最大值;
(3)若种草部分的面积不少于700m2,栽花部分的面积不少于100m2,请求出绿化总费用W的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】深圳市某校九年级有500名学生,在体育考试前随机抽取部分学生进行体能测试,成绩分别记为A、B、C、D共四个等级,其中A级和B级成绩为“优”,将测试结果绘制成如下条形统计图和扇形统计图.
成绩频数条形统计图 成绩频数扇形统计图
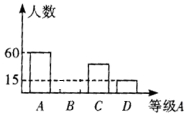
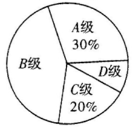
(1)求抽取参加体能测试的学生人数;
(2)补全条形统计图;
(3)估计该校九年级全体学生参加体能测试成绩为“优”的学生共有多少人?(精确到个位)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AB=BC,∠ABC=90°,以AB为直径的⊙O交OC与点D,AD的延长线交BC于点E,过D作⊙O的切线交BC于点F.下列结论:①CD2=CE·CB;②4EF 2=ED ·EA;③∠OCB=∠EAB;④![]() .其中正确的只有____________________.(填序号)
.其中正确的只有____________________.(填序号)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com