
【题目】为了预防流感,某学校在休息日用药熏消毒法对教室进行消毒. 已知药物释放过程中,室内每立方米空气中的含药量y(mg)与时间t(h)成正比;药物释放完毕后,y与t之间的函数解析式为y=![]() (a为常数),如图所示. 根据图中提供的信息,解答下列问题:
(a为常数),如图所示. 根据图中提供的信息,解答下列问题:
(1)写出从释放药物开始,y与t之间的两个函数解析式及相应的自变量取值范围;
(2)据测定,当空气中每立方米的含药量降低到0.25mg以下时,学生方可进入教室,那么药物释放开始,至少需要经过多少小时,学生才能进入教室?

 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:
【题目】如图所示,边长为1的正方形网格中,△ABC的三个顶点A、B、C都在格点上.
(1)作关于△ABC关于x轴的对称图形△DEF,(其中A、B、C的对称点分别是D、E、F),并写出点D坐标;
(2)P为x轴上一点,请在图中画出使△PAB的周长最小时的点P,并直接写出此时点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC=5,cos∠ABC=0.6,将△ABC绕点C顺时针旋转,得到△A1B1C.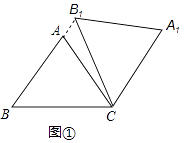
(1)如图1,当点B1在线段BA延长线上时.①求证:BB1∥CA1;②求△AB1C的面积;
(2)如图2,点E是BC边的中点,点F为线段AB上的动点,在△ABC绕点C顺时针旋转过程中,点F的对应点是F1 , 求线段EF1长度的最大值与最小值的差.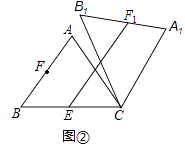
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图①在△ABC中,点D是BC边上的一点,将△ABD沿AD折叠,得到△AED,AE与BC交于点F.已知∠B=50°,∠BAD=15°,求∠AFC的度数.
(2)如图②,将△ABC纸片沿DE折叠,使点A落在四边形BCED的内部点A′的位置,∠1、∠2与∠A之间存在一定的数量关系,请判断它们之间的关系,并说明理由.
(3)如图③,将△ABC纸片沿DE折叠,使点A落在四边形BCED的外部点A′的位置,此时∠1、∠2与∠A之间也存在一定的数量关系,请直接写出它们之间的关系,无需说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市公交公司为应对春运期间的人流高峰,计划购买A、B两种型号的公交车共10辆,若购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车2辆,B型公交车3辆,共需650万元,
(1)试问该公交公司计划购买A型和B型公交车每辆各需多少万元?
(2)若该公司预计在某条线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次.若该公司购买A型和B型公交车的总费用W不超过1200万元,且确保这10辆公交车在某条线路的年均载客量总和不少于680万人次,则该公司有哪几种购车方案?哪种购车方案的总费用W最少?最少总费用是多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,BC为⊙O的切线,D为⊙O上的一点,CD=CB,延长CD交BA的延长线于点E. 
(1)求证:CD为⊙O的切线;
(2)若BD的弦心距OF=1,∠ABD=30°,求图中阴影部分的面积.(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰△ABC中,AB=AC=8,BC=5,AB的垂直平分线DE交AB于点D,交AC于点E,则△BEC的周长为( ) 
A.13
B.14
C.15
D.16
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用两个边长为15![]() 的小正方形拼成一个大的正方形,
的小正方形拼成一个大的正方形,
(1)求大正方形的边长?
(2)若沿此大正方形边的方向剪出一个长方形,能否使剪出的长方形纸片的长宽之比为4:3,且面积为720cm2?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.

(1)求证:△ABE≌△CBF;
(2)若∠CAE=30°,求∠ACF的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com