
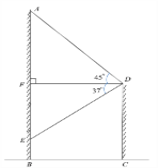
【题目】如图,在建筑物AB上,挂着35 m长的宣传条幅AE,从另一建筑物CD的顶部D处看条幅顶端A处,仰角为45°,看条幅底端E处,俯角为37°.求两建筑物间的距离BC.
(参考数据:sin37°≈0.6,cos37°≈0.8, tan37°≈0.75)

【答案】两建筑物间的距离BC为20m
【解析】试题分析:
如图,过点D作DF![]() AB交AB于点F,则∠DFA=∠DFE=90°,结合已知条件易得AF=DF,EF=DF·tan37°,结合AE=AF+EF=35即可列出方程解得DF的长,这样由四边形BCDF是矩形即可得到BC=DF从而求出BC的长了.
AB交AB于点F,则∠DFA=∠DFE=90°,结合已知条件易得AF=DF,EF=DF·tan37°,结合AE=AF+EF=35即可列出方程解得DF的长,这样由四边形BCDF是矩形即可得到BC=DF从而求出BC的长了.
试题解析:
过点D作DF![]() AB交AB于点F,
AB交AB于点F,
∴∠DFA=∠DFE=90°,
∵∠ABC=∠BCD=90°,
∴四边形BCDF是矩形,
∴BC=DF,
∵在Rt△ADF中,∠ADF=45°,
∴AF=DF,
∵在Rt△DFE中,∠EDF=37°,
∴EF=DF·tan37°,
又∵AF+EF=AE=35,
∴DF+DF·tan37°=35,
解得DF=BC=20(m)
答:两建筑物间的距离BC为20m.


科目:初中数学 来源: 题型:
【题目】已知:如图,折叠矩形ABCD,使点B落在对角线AC上的点F处,若BC=8,AB=6,则线段CE的长度是( )

A. 3 B. 4 C. 5 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
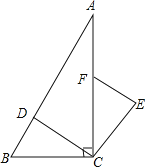
【题目】如图,在Rt△ABC中,∠ACB=90°,点D,F分别在AB,AC上,CF=CB.连接CD,将线段CD绕点C按顺时针方向旋转90°后得CE,连接EF.
(1)求证:△BCD≌△FCE;
(2)若EF∥CD.求∠BDC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景区的水上乐园有一批![]() 人座的自划船,每艘可供
人座的自划船,每艘可供![]() 至
至![]() 位游客乘坐游湖,因景区加大宣传,预计今年游客将会增加.水上乐园的工作人员在去年
位游客乘坐游湖,因景区加大宣传,预计今年游客将会增加.水上乐园的工作人员在去年![]() 月
月![]() 日一天出租的
日一天出租的![]() 艘次
艘次![]() 人自划船中随机抽取了
人自划船中随机抽取了![]() 艘,对其中抽取的每艘船的乘坐人数进行统计,并制成如下统计图.
艘,对其中抽取的每艘船的乘坐人数进行统计,并制成如下统计图.
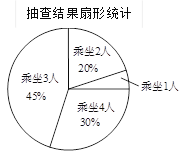
(1)求扇形统计图中, “乘坐1人”所对应的圆心角度数;
(2)估计去年![]() 月
月![]() 日这天出租的
日这天出租的![]() 艘次
艘次![]() 人自划船平均每艘船的乘坐人数;
人自划船平均每艘船的乘坐人数;
(3)据旅游局预报今年![]() 月
月![]() 日这天该景区可能将增加游客300人,请你为景区预计这天需安排多少艘4人座的自划船才能满足需求.
日这天该景区可能将增加游客300人,请你为景区预计这天需安排多少艘4人座的自划船才能满足需求.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】.观察下列算式特点:
①13=12
②13+23=32
③13+23+33=62
④13+23+33+43=102
⑤13+23+33+43+53=152…
(1)请你写出第⑥个算式;
(2)用含n(n为正整数)的式子表示第n个算式;
(3)请用上述规律计算:73+83+93+…+123.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
![]()
![]()
![]()
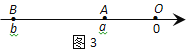
点A、B在数轴上分别表示实数a、b,A、B两点之间的距离表示为∣AB∣.当A、B两点中有一点在原点时,不妨设点A在原点,如图1,∣AB∣=∣OB∣=∣b∣=∣a-b∣;当A、B两点都不在原点时,如图2,点A、B都在原点的右边∣AB∣=∣OB∣-∣OA∣=∣b∣-∣a∣=![]() =∣a-b∣;如图3,当点A、B都在原点的左边,∣AB∣=∣OB∣-∣OA∣=∣b∣-∣a∣=
=∣a-b∣;如图3,当点A、B都在原点的左边,∣AB∣=∣OB∣-∣OA∣=∣b∣-∣a∣=![]() =∣a-b∣;如图4,当点A、B在原点的两边,∣AB∣=∣OB∣+∣OA∣=∣a∣+∣b∣=
=∣a-b∣;如图4,当点A、B在原点的两边,∣AB∣=∣OB∣+∣OA∣=∣a∣+∣b∣=![]() =∣a-b∣.
=∣a-b∣.
回答下列问题:
(1)数轴上表示2和5的两点之间的距离是_____,数轴上表示1和-3的两点之间的距离是______.
(2)数轴上若点A表示的数是x,点B表示的数是-2,则点A和B之间的距离是_____,若∣AB∣=2,那么x为______.
(3)当x是_____时,代数式![]() .
.
(4)若点A表示的数是-1,点B与点A的距离是10,且点B在点A的右侧,动点P、Q同时从A、B出发沿数轴正方向运动,点P的速度是每秒3个单位长度,点Q的速度是每秒![]() 个单位长度,求运动几秒后,点P与点Q之间的距离为5个单位长度 ?(请写出必要的求解过程)
个单位长度,求运动几秒后,点P与点Q之间的距离为5个单位长度 ?(请写出必要的求解过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有三条格点线段AB、CD、DE(线段的端点是网格线的交点),它们组成的图形不是轴对称图形.现要通过平移或旋转,改变其中一条线段的位置,使运动后的这条线段与另两条线段组成一个轴对称图形.请分别填写三种平移方案和三种旋转方案平移方案:(移动方向限填“上”、“下”、“左”、“右”)
(1)将线段 向 平移1格;
(2)将线段 向 平移1格;
(3)将线段 向 平移1格;
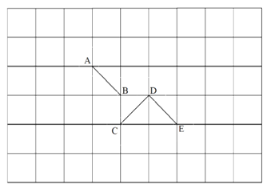
旋转方案:(限填绕A、B、C、D、E中的一点旋转且任意两条线段不重合)
(4)将线段 绕点 按 时针方向旋转 度;
(5)将线段 绕点 按 时针方向旋转 度;
(6)将线段 绕点 按 时针方向旋转 度;
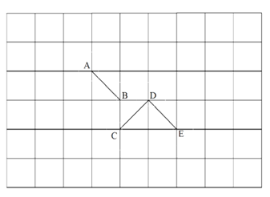
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD的对角线AC,BD相交于点O,AE=CF.
(1)求证:△BOE≌△DOF;
(2)连接DE,BF,若BD⊥EF,试探究四边形EBFD的形状,并对结论给予证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
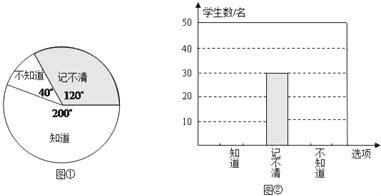
【题目】今年苏州市在全市中小学中开展以感恩和生命为主题的教育活动,各中小学结合学生实际,开展了形式多样的感恩教育活动.下面图①,图②分别是某校调查部分学生是否知道母亲生日情况的扇形统计图和条形统计图.根据图上信息,解答下列问题:
(1)求本次被调查学生的人数,并补全条形统计图;
(2)若全校共有2700名学生,你估计这所学校有多少名学生知道母亲的生日?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com