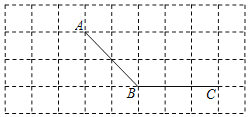
【题目】如图，所有小正方形的边长都为1个单位，A、B、C均在格点上．
过点C画线段AB的平行线CD；
过点A画线段BC的垂线，垂足为E；
过点A画线段AB的垂线，交线段CB的延长线于点F；
线段AE的长度是点______到直线______的距离；
线段AE、BF、AF的大小关系是______
用“
”连接
科目：初中数学 来源： 题型：
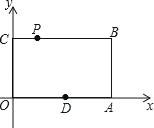
【题目】如图，在平面直角坐标系中，矩形OABC的顶点A、C的坐标分别为（6，0）、（0，4），点P是线段BC上的动点，当△OPA是等腰三角形时，则P点的坐标是_____．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】观察下列等式：
，
，
，则以上三个等式两边分别相加得：
．
观察发现
______；
______．
拓展应用
有一个圆，第一次用一条直径将圆周分成两个半圆
如图
，在每个分点标上质数m，记2个数的和为
；第二次再将两个半圆周都分成
圆周如图
，在新产生的分点标上相邻的已标的两数之和的
，记4个数的和为
；第三次将四个圆周分成
圆周如图
，在新产生的分点标上相邻的已标的两数之和的
，记8个数的和为
；第四次将八个圆周分成
圆周，在新产生的分点标上相邻的已标的两个数的和的，记16个数的和为
；
如此进行了n次．
______用含m、n的代数式表示
；
当
时，求
的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】我国淡水资源短缺问题十分突出，已成为我国经济和社会可持续发展的重要制约因素，节约用水是各地的一件大事．某校初三学生为了调查居民用水情况，随机抽查了某小区20户家庭的月用水量，结果如表所示：
(1)求这20户家庭月用水量的平均数、众数及中位数．
(2)政府为了鼓励节约用水，拟试行水价浮动政策．即设定每个家庭月基本用水量a(t)，家庭月用水量不超过a(t)的部分按原价收费，超过a(t)的部分加倍收费．
①你认为以平均数作为该小区的家庭月基本用水量a(t)合理吗？为什么？(简述理由)
②你认为该小区的家庭月基本用水量a(t)为多少时较为合理？为什么？(简述理由)
查看答案和解析>>
科目：初中数学 来源： 题型：
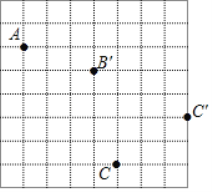
【题目】画图并填空：如图，方格纸中每个小正方形的边长都为1，在方格纸中将△ABC经过一次平移后得到△A′B′C′，图中标出来点A，点B′、点C和它的对应点C′．
（1）请画出平移前后的△ABC和△A′B′C′；(注意并标注好字母)
（2）利用网格画出△ABC中BC边上的中线AD；(注意并标注好字母)
（3）利用网格画出△ABC中AB边上的高CE；(注意并标注好字母)
（4）△A′B′C′的面积为 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
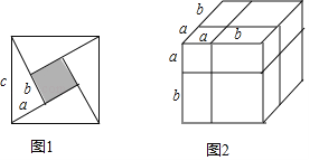
【题目】（知识生成）
我们已经知道，通过不同的方法表示同一图形的面积，可以探求相应的等式．
2002年8月在北京召开了国际数学大会，大会会标如图1所示，它是由四个形状大小完全相同的直角三角形与中间的小正方形拼成的一个大正方形，直角三角形的两条直角边长分别为a、b （ a<b ），斜边长为c．
（1）图中阴影部分的面积用两种方法可分别表示为 、 ；
（2）你能得出的a，b，c之间的数量关系是 （等号两边需化为最简形式）；
（3）一直角三角形的两条直角边长为6和8，则其斜边长为 ．
（知识迁移）
通过不同的方法表示同一几何体的体积，也可以探求相应的等式．如图2是边长为a+b的正方体，被如图所示的分割线分成8块．
（4）用不同方法计算这个正方体体积，就可以得到一个等式，这个等式可以为 ．（等号两边需化为最简形式）
（5）已知a+b＝3，ab＝1，利用上面的规律求a3+b3的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某开发公司要生产若干件新产品，需要精加工后，才能投放市场，现有红星和巨星两家加工厂都想加工这批产品，已知红星厂单独加工比巨星厂单独加工这批产品多用20天，红星厂每天可加工16件产品，巨星厂每天可加工24件产品，公司需付给红星厂每天加工费800元，付给巨星厂每天加工费1200元．
这个公司要加工多少件新产品？
公司的产品可由一家工厂单独加工完成，也可由两家工厂合作完成，在加工过程中公司需另派一名工程师每天到厂家进行指导，并支付工程师每天10元的午餐补助，请你帮助公司从所有可供选择的方案中，选择一种既省钱又省时的加工方案．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某社区超市第一次用6000元购进甲、乙两种商品，其中乙商品的件数比甲商品件数的
倍多15件，甲、乙两种商品的进价和售价如下表：（注：获利＝售价﹣进价）
甲 | 乙 | |
进价（元/件） | 22 | 30 |
售价（元/件） | 29 | 40 |
（1）该超市购进甲、乙两种商品各多少件？
（2）该超市将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润？
（3）该超市第二次以第一次的进价又购进甲、乙两种商品，其中甲商品的件数不变，乙商品的件数是第一次的3倍；甲商品按原价销售，乙商品打折销售，第二次两种商品都销售完以后获得的总利润比第一次获得的总利润多180元，求第二次乙商品是按原价打几折销售？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，正方形ABCD中，G为BC边上一点，BE⊥AG于E，DF⊥AG于F，连接DE．
（1）求证：△ABE≌△DAF；
（2）若AF=1，四边形ABED的面积为6，求EF的长．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
