
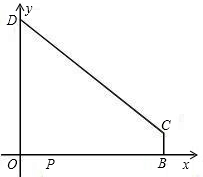
| CD2-CE2 |
| 102-82 |
|
|
| 25 |
| 28 |
| 221 |
| 28 |
|
|
| 1 |
| 4 |
| 11 |
| 4 |
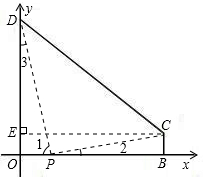


科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
2
| ||
| x |
| 1 |
| 2 |

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| PM |
| BE |
| PN |
| AD |
| PA |
| PB |
| EF |
| EG |
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
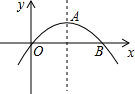
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| 销售价x(元/kg) | … | 25 | 24 | 23 | 22 | … |
| 销售量y(kg) | … | 2000 | 2500 | 3000 | 3500 | … |

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
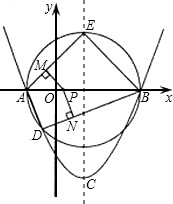
 满足AB∥x轴,点C是抛物线的顶点.
满足AB∥x轴,点C是抛物线的顶点.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
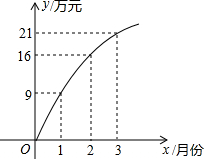
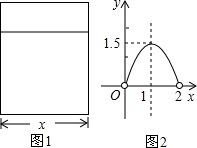 积为ym2,y与x的函数图象如图2所示.
积为ym2,y与x的函数图象如图2所示.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| 1 |
| 2 |
| 9 |
| 8 |
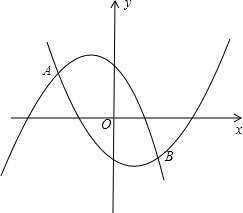 两点,试问当x为何值时,线段CD有最大值,其最大值为多少?
两点,试问当x为何值时,线段CD有最大值,其最大值为多少?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com