
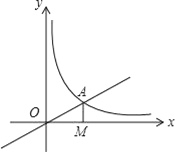
【题目】如图,直线OA:y=![]() x的图象与反比例函数y=
x的图象与反比例函数y=![]() (k≠0)在第一象限的图象交于A点,过A点作轴的垂线,垂足为M,已知△OAM的面积为1.
(k≠0)在第一象限的图象交于A点,过A点作轴的垂线,垂足为M,已知△OAM的面积为1.
(1)求反比例函数的解析式;
(2)如果B为反比例函数在第一象限图象上的点(点B与点A不重合),且B点的横坐标为1,在x轴上求一点P,使PA+PB最小.
【答案】(1)y=![]() ;(2)P点的坐标为(
;(2)P点的坐标为(![]() ,0).
,0).
【解析】
(1)设点A的坐标为(a,b),由点A在反比例函数图象上结合三角形△OAM的面积为1,可得出关于k、a、b的三元一次方程组,解方程即可求出k值,从而得出反比例函数解析式;
(2)联立直线与反比例函数解析式求出点A的坐标,找出点A关于x轴的对称点C的坐标,再结合反比例函数解析式求出点B坐标,连接BC即可找出点P的位置,由点B、C的坐标利用待定系数法即可求出直线BC的解析式,令y=0求出x值即可得出点P的坐标.
解:(1)设点A的坐标为(a,b),
则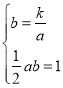 ,解得:k=2.
,解得:k=2.
∴反比例函数的解析式为y=![]() .
.
(2)联立直线OA和反比例函数解析式得:
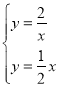 ,解得:
,解得:![]() .
.
∴点A的坐标为(2,1).
设A点关于x轴的对称点为C,则C点的坐标为(2,﹣1),连接BC较x轴于点P,点P即为所求.如图所示.
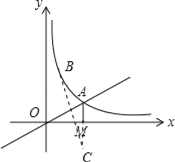
设直线BC的解析式为y=mx+n,
由题意可得:B点的坐标为(1,2),
∴![]() ,
,
解得:![]() .
.
∴BC的解析式为y=﹣3x+5.
当y=0时,0=﹣3x+5,解得:x=![]() .
.
∴P点的坐标为(![]() ,0).
,0).


科目:初中数学 来源: 题型:
【题目】某超市预测某饮料有发展前途,用1600元购进一批饮料,面市后果然供不应求,又用6000元购进这批饮料,第二批饮料的数量是第一批的3倍,但单价比第一批贵2元.
(1)第一批饮料进货单价多少元?
(2)若二次购进饮料按同一价格销售,两批全部售完后,获利不少于1200元,那么销售单价至少为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一只不透明袋子中装有三只大小、质地都相同的小球,球面上分别标有数字1、﹣2、3,搅匀后先从中任意摸出一个小球(不放回),记下数字作为点A的横坐标,再从余下的两个小球中任意摸出一个小球,记下数字作为点A的纵坐标.
(1)用画树状图或列表等方法列出所有可能出现的结果;
(2)求点A落在第四象限的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
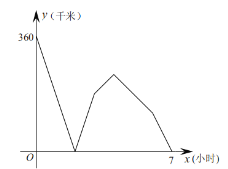
【题目】快、慢两车分别从相距![]() 千米路程的甲、乙两地同时出发,匀速行驶.先相向而行,快车到达乙地后,停留
千米路程的甲、乙两地同时出发,匀速行驶.先相向而行,快车到达乙地后,停留![]() 小时,然后按原路原速返回,快车比慢车晚
小时,然后按原路原速返回,快车比慢车晚![]() 小时到达甲地,快、慢两车之间相距的距离
小时到达甲地,快、慢两车之间相距的距离![]() (千米)与出发后所用的时间
(千米)与出发后所用的时间![]() (小时)的关系如图所示,请问:在快车返回途中,快、慢两车相距路程为
(小时)的关系如图所示,请问:在快车返回途中,快、慢两车相距路程为![]() 千米时,慢车行驶了__________小时.
千米时,慢车行驶了__________小时.
查看答案和解析>>
科目:初中数学 来源: 题型:
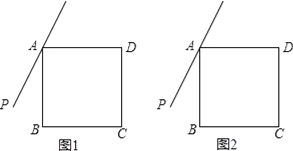
【题目】在正方形ABCD外侧作直线AP,点B关于直线AP的对称点为E,连接BE,DE,其中DE交直线AP于点F.
(1)①依题意补全图1;
②若∠PAB=20°,求∠ADF的度数;
(2)若设∠PAB=a,且0°<a<90°,求∠ADF的度数(直接写出结果,结果可用含a的代数式表示)
(3)如图2,若45°<∠PAB<90°,用等式表示线段AB、FE、FD之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班“数学兴趣小组”对函数y=x2﹣2|x|的图象和性质进行了探究,探究过程如下.
(1)补全下表,在所给坐标系中画出函数的图象:
x | … | ﹣3 | ﹣ | ﹣2 | ﹣1 | 0 | 1 | 2 |
| 3 | … |
y | … | 3 |
| 0 | ﹣1 | 0 | … |
(2)观察图象,写出该函数两条不同类型的性质;
(3)进一步探究函数图象发现:
①函数图象与x轴有 个交点,所以对应方程x2﹣2|x|=0有 个实数根;
②方程x2﹣2|x|=2有 个实数根;
③关于x的方程x2﹣2|x|=a有4个实数根,a的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“校园手机”现象越来越受到社会的关注.“五一”期间,小记者刘铭随机调查了城区若干名学生和家长对中学生带手机现象的看法,统计整理并制作了如下的统计图:
(1)求这次调查的家长人数,并补全图①;
(2)求图②中表示家长“赞成”的圆心角的度数;
(3)如果该市有8万名初中生,持“无所谓”态度的学生大约有多少人?
(4)从这次接受调查的家长与学生中随机抽查一个,恰好是“无所谓”态度的概率是多少?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com