
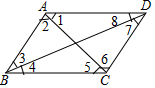
 如图,若AD∥BC,则∠1=∠5,∠8=∠4,∠ABC+∠BAC=180°;若DC∥AB,则∠3=∠7,∠2=∠6,∠ABC+∠BCD=180.
如图,若AD∥BC,则∠1=∠5,∠8=∠4,∠ABC+∠BAC=180°;若DC∥AB,则∠3=∠7,∠2=∠6,∠ABC+∠BCD=180. 科目:初中数学 来源: 题型:填空题
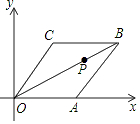 已知菱形OABC在平面直角坐标系的位置如图所示,顶点A(5,0),OB=4$\sqrt{5}$,点P是对角线OB上的一个动点,D(0,1),当CP+DP最短时,点P的坐标为($\frac{10}{7}$,$\frac{5}{7}$).
已知菱形OABC在平面直角坐标系的位置如图所示,顶点A(5,0),OB=4$\sqrt{5}$,点P是对角线OB上的一个动点,D(0,1),当CP+DP最短时,点P的坐标为($\frac{10}{7}$,$\frac{5}{7}$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
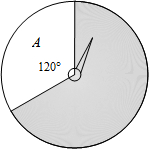 如图,有甲、乙两个相同的转盘,让两个转盘分别自由转动一次,当转盘停止转动(若指针指在边界处则重转),求
如图,有甲、乙两个相同的转盘,让两个转盘分别自由转动一次,当转盘停止转动(若指针指在边界处则重转),求查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com