
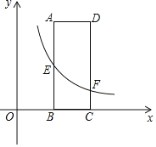
【题目】如图,矩形ABCD的两边AD,AB的长分别为3,8,E是AB的中点,反比例函数y=![]() 的图象经过点E,与CD交于点F.
的图象经过点E,与CD交于点F.
(1)若点C坐标为(6,0),求m的值及图象经过D,E两点的直线解析式;
(2)若DF﹣DE=2,求反比例函数的表达式.
【答案】(1)m=12,![]() ;(2)y=
;(2)y=![]() .
.
【解析】
(1)根据矩形的性质,可得D,E点坐标,根据待定系数法,可得答案;
(2)根据勾股定理,可得DE的长,根据线段的和差,可得DF,进而可得F点坐标,根据待定系数法,可得m的值,可得答案.
(1)∵点C坐标为(6,0),AD=3,AB=8,E为AB的中点,
∴点D(6,8),E(3,4),
∵反比例函数图象经过E点,
∴m=3×4=12,
设直线DE的解析式为:y=kx+b,
则![]() ,解得
,解得![]() ,
,
∴一次函数的解析式为:![]() ;
;
(2)∵AD=3,AE=4,
∴DE=![]() ,
,
∵DF﹣DE=2,
∴DF=7,CF=1,
设E点坐标为(a,4),则F点坐标为(a+3,1),
∵E,F两点在函数y=![]() 图象上,
图象上,
∴4a=a+3,解得:a=1.
∴E(1,4),
∴m=1×4=4,
∴反比例函数的表达式为y=![]() .
.


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:
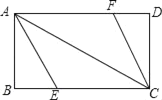
【题目】同学张丰用一张长18cm、宽12cm矩形纸片折出一个菱形,他沿矩形的对角线AC折出∠CAE=∠DAC,∠ACF=∠ACB的方法得到四边形AECF(如图).
(1)证明:四边形AECF是菱形;
(2)求菱形AECF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市要选拔一名教师参加省级评优课比赛:经笔试、面试,结果小潘和小丁并列第一,评委会决定通过摸球来确定人选.规则如下:在不透明的布袋里装有除颜色之外均相同的2个红球和1个蓝球,小潘先取出一个球,记住颜色后放回,然后小丁再取出一个球.若两次取出的球都是红球,则小潘胜出;若两次取出的球是一红一蓝,则小丁胜出.你认为这个规则对双方公平吗?请用列表法或画树状图的方法进行分析.
查看答案和解析>>
科目:初中数学 来源: 题型:
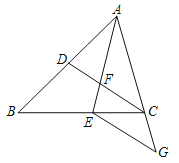
【题目】如图,在△ABC中,点D、E分别在边AB、BC上,AE与CD交于点F,若AE平分∠BAC,ABAF=ACAE.
(1)求证:∠AFD=∠AEC;
(2)若EG∥CD,交边AC的延长线于点G,求证:CDCG=FCBD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=﹣x+5的图象与反比例函数![]() (k≠0)在第一象限的图象交于A(1,n)和B两点.
(k≠0)在第一象限的图象交于A(1,n)和B两点.

(1)求反比例函数的解析式及点B坐标;
(2)在第一象限内,当一次函数y=-x+5的值大于反比例函数![]() (k≠0)的值时,写出自变量x的取值范围.
(k≠0)的值时,写出自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数的图象经过点A(2,6).
(1)求这个反比例函数的解析式;
(2)这个函数的图象位于哪些象限?y随x的增大如何变化?
(3)点B(3,4),C(5,2),D(![]() ,
,![]() )是否在这个函数图象上?为什么?
)是否在这个函数图象上?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() .以
.以![]() 为直径的
为直径的![]() 与
与![]() 交于点
交于点![]() ,与
,与![]() 交于点
交于点![]() ,点
,点![]() 在边
在边![]() 的延长线上,且
的延长线上,且![]() .
.
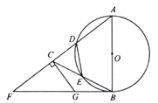
(1)试说明![]() 是
是![]() 的切线;
的切线;
(2)过点![]() 作
作![]() ,垂足为
,垂足为![]() .若
.若![]() ,
,![]() ,求
,求![]() 的半径;
的半径;
(3)连接![]() ,设
,设![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
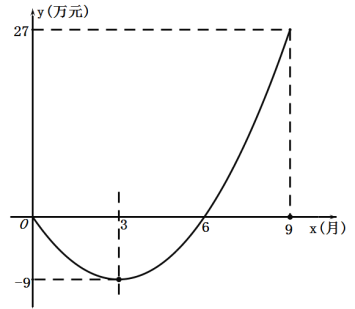
【题目】大学生小李和同学一起自主创业开办了一家公司,公司对经营的盈亏情况在每月的最后一天结算一次.在1-12月份中,该公司前x个月累计获得的总利润y(万元)与销售时间x(月)之间满足二次函数关系.
(1)求y与x函数关系式.
(2)该公司从哪个月开始“扭亏为盈”(当月盈利)? 直接写出9月份一个月内所获得的利润.
(3)在前12 个月中,哪个月该公司所获得利润最大?最大利润为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=8,BC=6,以边AB的中点O为圆心,作半圆与AC相切于点M,P、Q分别是边BC和半圆上的动点,连接PQ,则PQ长的最小值是( )

A.1B.2C.3D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com