
如图所示(1),OA,OB是⊙O的两条半径,且OA⊥OB,点C是OB延长线上任意一点,过点C作CD切⊙O于点D,连接AD交OC于点E.
求证:CD=CE.
(1)若将如图所示(1)中的半径OB所在直线向上平移交OA于点F,交⊙O于点![]() ,其他条件不变(如图所示(2)),那么上述结论CD=CE还成立吗?为什么?
,其他条件不变(如图所示(2)),那么上述结论CD=CE还成立吗?为什么?
(2)若将如图所示(1)中的半径OB所在直线向上平移到⊙O外的CF,点E是DA的延长线与CF的交点,其他条件不变(如图所示(3)),那么上述结论CD=CE还成立吗?为什么?

|
证明:连接OD. 因为CD是⊙O的切线, 所以OD⊥CD, 所以∠ADO+∠ADC= 因为OA⊥OB, 所以∠DAO+∠AEO= 因为∠ADO=∠DAO, 所以∠ADC=∠AEO=∠CED, 所以CD=CE. (1)CD=CE仍然成立.证明如下: 连接OD. 因为CD是⊙O的切线, 所以OD⊥CD, 所以∠ADO+∠ADC= 因为OA⊥CF, 所以∠DAO+∠AEF= 因为∠ADO=∠DAO, 所以∠ADC=∠AEF=∠CED, 所以CD=CE. (2)CD=CE仍然成立.证明如下: 连接OD,延长OA交CF于点G. 因为CD是⊙O的切线, 所以OD⊥CD, 所以∠ADO+∠ADC= 因为OA⊥CF, 所以∠EAG+∠AEG= 因为∠ADO=∠DAO=∠EAG, 所以∠ADC=∠AEG, 即∠CDE=∠CED, 所以CD=CE. |


科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
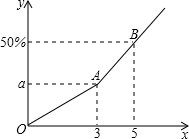 (2013•宜昌模拟)某工程队做一项工作,工作时间x(天)和完成工作的百分比y的关系如图所示,其中线段OA所在直线的函数关系式是y=
(2013•宜昌模拟)某工程队做一项工作,工作时间x(天)和完成工作的百分比y的关系如图所示,其中线段OA所在直线的函数关系式是y=| 1 | 12 |
查看答案和解析>>
科目:初中数学 来源: 题型:
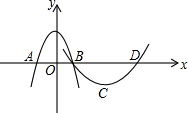 二次函数y1=ax2-2bx+c和y2=(a+1)•x2-2(b+2)x+c+3在同一坐标系中的图象如图所示,若OB=OA,BC=DC,且点B,C的横坐标分别为1,3,求这两个函数的解析式.
二次函数y1=ax2-2bx+c和y2=(a+1)•x2-2(b+2)x+c+3在同一坐标系中的图象如图所示,若OB=OA,BC=DC,且点B,C的横坐标分别为1,3,求这两个函数的解析式.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com