
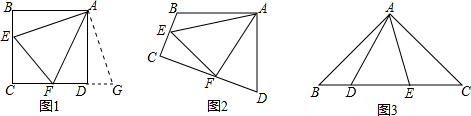
分析 (1)①根据旋转的性质得出AE=AG,∠BAE=∠DAG,BE=DG,求出∠EAF=∠GAF=45°,根据SAS推出△EAF≌△GAF,根据全等三角形的性质得出EF=GF,即可求出答案;
②根据旋转的性质得出AE=AG,∠B=∠ADG,∠BAE=∠DAG,求出C、D、G在一条直线上,根据SAS推出△EAF≌△GAF,根据全等三角形的性质得出EF=GF,即可求出答案;
(2)根据等腰直角三角形性质好勾股定理求出∠ABC=∠C=45°,BC=4,根据旋转的性质得出AF=AE,∠FBA=∠C=45°,∠BAF=∠CAE,求出∠FAD=∠DAE=45°,证△FAD≌△EAD,根据全等得出DF=DE,设DE=x,则DF=x,BF=CE=3-x,根据勾股定理得出方程,求出x即可.
解答 (1)①解:如图1,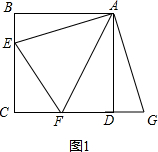
∵把△ABE绕点A逆时针旋转90°至△ADG,使AB与AD重合,
∴AE=AG,∠BAE=∠DAG,BE=DG,
∵∠BAD=90°,∠EAF=45°,
∴∠BAE+∠DAF=45°,
∴∠DAG+∠DAF=45°,
即∠EAF=∠GAF=45°,
在△EAF和△GAF中
$\left\{\begin{array}{l}{AF=AF}\\{∠EAF=∠GAF}\\{AE=AG}\end{array}\right.$
∴△EAF≌△GAF(SAS),
∴EF=GF,
∵BE=DG,
∴EF=GF=BE+DF;
②解:∠B+∠D=180°,
理由是: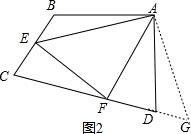
把△ABE绕A点旋转到△ADG,使AB和AD重合,
则AE=AG,∠B=∠ADG,∠BAE=∠DAG,
∵∠B+∠ADC=180°,
∴∠ADC+∠ADG=180°,
∴C、D、G在一条直线上,
和①知求法类似,∠EAF=∠GAF=45°,
在△EAF和△GAF中
$\left\{\begin{array}{l}{AF=AF}\\{∠EAF=∠GAF}\\{AE=AG}\end{array}\right.$
∴△EAF≌△GAF(SAS),
∴EF=GF,
∵BE=DG,
∴EF=GF=BE+DF;
故答案为:∠B+∠D=180°;
(2)解:∵△ABC中,AB=AC=2$\sqrt{2}$,∠BAC=90°,
∴∠ABC=∠C=45°,由勾股定理得:BC=$\sqrt{A{B}^{2}+A{C}^{2}}$=$\sqrt{(2\sqrt{2})^{2}+(2\sqrt{2})^{2}}$=4,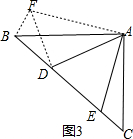
把△AEC绕A点旋转到△AFB,使AB和AC重合,连接DF.
则AF=AE,∠FBA=∠C=45°,∠BAF=∠CAE,
∵∠DAE=45°,
∴∠FAD=∠FAB+∠BAD=∠CAE+∠BAD=∠BAC-∠DAE=90°-45°=45°,
∴∠FAD=∠DAE=45°,
在△FAD和△EAD中
$\left\{\begin{array}{l}{AD=AD}\\{∠FAD=∠EAD}\\{AF=AE}\end{array}\right.$
∴△FAD≌△EAD,
∴DF=DE,
设DE=x,则DF=x,
∵BC=1,
∴BF=CE=4-1-x=3-x,
∵∠FBA=45°,∠ABC=45°,
∴∠FBD=90°,
由勾股定理得:DF2=BF2+BD2,
x2=(3-x)2+12,
解得:x=$\frac{5}{3}$,
即DE=$\frac{5}{3}$.
点评 本题考查了旋转的性质,全等三角形的性质和判定,解直角三角形,勾股定理的应用,此题是开放性试题,首先在特殊图形中找到规律,然后再推广到一般图形中,对学生的分析问题,解决问题的能力要求比较高.


科目:初中数学 来源: 题型:解答题
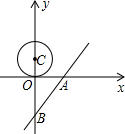 在平面直角坐标系中,点C的坐标为(0,1.5),我们把以点C为圆心,半径为1.5的圆称为点C的朋友圈,圆周上的每一个点叫做点C的一个好友.
在平面直角坐标系中,点C的坐标为(0,1.5),我们把以点C为圆心,半径为1.5的圆称为点C的朋友圈,圆周上的每一个点叫做点C的一个好友.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
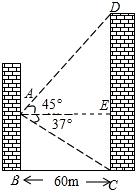 如图,物华大厦离小伟家60m,小伟从自家的窗中眺望大厦,并测得大厦顶部的仰角是45°,而大厦底部的俯角是37°,求该大厦的高度(结果精确到0.1米)
如图,物华大厦离小伟家60m,小伟从自家的窗中眺望大厦,并测得大厦顶部的仰角是45°,而大厦底部的俯角是37°,求该大厦的高度(结果精确到0.1米)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com