
分析 此题可以用数形结合来解题:x为数轴上的一点,|x-1|+|x-2|+|x-3|+…|x-2017|表示:点x到数轴上的2017个点(1、2、3、…、2017)的距离之和,由于原式的绝对值共有2017项,最中间的那一项是|x-1009|,所以只需取x=1009,它们的和就可以获得最小值.
解答 解:由于原式的绝对值共有2017项,最中间的那一项是|x-1009|,所以只需取x=1009,它们的和就可以获得最小值,原式可以展开为:
|x-1|+|x-2|+|x-3|+…+|x-2017|
=|1009-1|+|1009-2|+…+|1009-1009|+|1009-1010|+…+|1009-2017|
=1008+…+1+0+1+…+1008
=2×(1+2+3+…+1008)
=1017072.
故答案为:1017072,1009.
点评 此题主要考查了绝对值的性质以及利用数形结合求最值问题,利用已知得出x=1009时,|x-1|+|x-2|+|x-3|+…|x-2017|能够取到最小值是解题关键.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:解答题
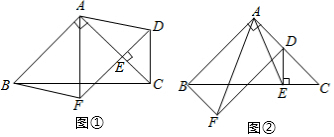
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
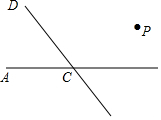 如图,直线CD与直线AB相交于C.
如图,直线CD与直线AB相交于C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com