
如图,在△ABC中,AB=AC=10,∠B=30°,O是线段AB上的一个动点,以O为圆心,OB为半径作⊙O交BC于点D,过点D作直线AC的垂线,垂足为E.
(1)求证:DE是⊙O的切线;
(2)设OB=x,求∠ODE的内部与△ABC重合部分的面积y的最大值.

科目:初中数学 来源:贵州省遵义市桐梓县2016-2017学年七年级上学期期末考试数学试卷 题型:解答题
如图,线段AC=6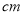 ,线段BC=15
,线段BC=15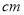 ,点M是AC的中点,在CB上取一点N,使得NB=2CN.
,点M是AC的中点,在CB上取一点N,使得NB=2CN.
(1)求CN的长?
(2)求MN的长?
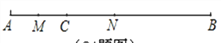
查看答案和解析>>
科目:初中数学 来源:云南省双柏县2017-2018学年上学期七年级期末数学试卷 题型:填空题
观察下列关于x的单项式,探究其规律:x,3x2,5x3,7x4,9 x5,11x6,…
按照上述规律,第2017个单项式是_________________.
4033x2017 【解析】【解析】 ∵第一个数x=x1; 第二个数3x2=(2×2﹣1)x2; 第三个数5x3=(2×3﹣1)x3; 第四个数7x4=(2×4﹣1)x4; 第五个数9x5=(2×5﹣1)x5; ∴第n个数为:(2n﹣1)xn. ∴第2017个单项式是(2×2017﹣1)x2017=4033x2017. 故答案为:4033x2017...查看答案和解析>>
科目:初中数学 来源:云南省双柏县2017-2018学年八年级上期期末数学试卷 题型:单选题
一次函数y=kx+b,当k<0,b<0时的图象大致位置是( )
A.  B.
B. 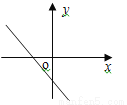
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源:云南省双柏县2017-2018学年八年级上期期末数学试卷 题型:填空题
使 有意义的x的取值范围为______.
有意义的x的取值范围为______.
查看答案和解析>>
科目:初中数学 来源:江苏省南京市联合体2018届九年级上学期期末考试数学试卷 题型:解答题
如图,大圆的弦AB、AC分别切小圆于点M、N.
(1)求证:AB=AC;
(2)若AB=8,求圆环的面积.

查看答案和解析>>
科目:初中数学 来源:江苏省南京市联合体2018届九年级上学期期末考试数学试卷 题型:填空题
如图,以正六边形ADHGFE的一边AD为边向外作正方形ABCD,则∠BED=_______°.

查看答案和解析>>
科目:初中数学 来源:山东省东营市河口区2017-2018学年度第一学期期末考试九年级数学试卷 题型:解答题
如图,点C在以AB为直径的⊙O上,AD与过点C的切线垂直,垂足为点D,AD交⊙O于点E.
(1) 求证:AC平分∠DAB;
(2) 连接BE交AC于点F,若cos∠CAD= ,求
,求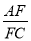 的值.
的值.

查看答案和解析>>
科目:初中数学 来源:北京大学附属中学2017-2018学年七年级上学期期中考试数学试卷 题型:单选题
单项式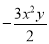 的系数与次数分别是( ).
的系数与次数分别是( ).
A.  ,
, 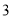 B.
B.  ,
,  C.
C.  ,
, 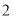 D.
D.  ,
, 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com