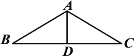
【题目】如图是人字型金属屋架的示意图，该屋架由BC、AC、BA、AD四段金属材料焊接而成，其中A、B、C、D四点均为焊接点，且AB=AC，D为BC的中点，假设焊接所需的四段金属材料已截好，并已标出BC段的中点D，那么，如果焊接工身边只有可检验直角的角尺，而又为了准确快速地焊接，他应该首先选取的两段金属材料及焊接点是（ ）
A.AB和AD，点AB.AB和AC，点B
C.AC和BC, 点CD.AD和BC，点D
科目：初中数学 来源： 题型：
【题目】某天下午，出租车司机小李始终在一条南北方向的商业大道上运营，如果规定向北为正方向，他记录的出租车行车里程如下（单位：千米）：
，
，
，
，
，
，
，
（
）将最后一名乘客送到目的地时，小李在出车地点的什么方向？距离是多少？
（
）若出租车每千米耗油量为
升，那么这天下午小李的出租车共耗油多少升？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在矩形ABCD中，AB＝4，BC＝10，E是直线AD上任意一点（不与点A重合），点A关于直线BE的对称点为A′，AA′所在直线与直线BC交于点F．
（1）如图①，当点E在线段AD上时，①若△ABE ∽△DEC，求AE的长；
②设AE＝x，BF＝y，求y与x的函数表达式．
（2）线段DA′的取值范围是 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，把Rt△ABC绕顶点C顺时针旋转90°得到Rt△DFC，若直线DF垂直平分AB，垂足为点E，连接BF，CE，且BC=2．下面四个结论：
①BF=
；
②∠CBF=45°；
③∠CED=30°；
④△ECD的面积为
，
其中正确的结论有_____．(填番号)
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知∠1＋∠2﹦180°,∠3﹦∠B，则DE∥BC，下面是王华同学的推导过程﹐请你帮他在括号内填上推导依据或内容．
证明：
∵∠1＋∠2﹦180（已知），
∠1﹦∠4 （_________________），
∴∠2﹢_____﹦180°.
∴EH∥AB（___________________________________）．
∴∠B﹦∠EHC（________________________________）．
∵∠3﹦∠B（已知）
∴ ∠3﹦∠EHC（____________________）．
∴ DE∥BC（__________________________________）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小明某天上午9时骑自行车离开家,15时回到家,他有意描绘了离家的距离与时间的变化情况(如图所示).
(1)图象表示了哪两个变量的关系?哪个是自变量?哪个是因变量?
(2)10时和13时,他分别离家多远?
(3)他到达离家最远的地方是什么时间?离家多远?
(4)11时到12时他行驶了多少千米?
(5)他可能在哪段时间内休息,并吃午餐?
(6)他由离家最远的地方返回时的平均速度是多少?
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下面是“过圆外一点作圆的切线”的尺规作图过程.
请回答以下问题：
（1）连接OA，OB，可证∠OAP =∠OBP = 90°，理由是______________________；
（2）直线PA，PB是⊙O的切线，依据是__________________________________．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，点A，B的坐标分别为A（0，a），B（b，a），且a，b满足（a﹣3）2+|b﹣6|＝0，现同时将点A，B分别向下平移3个单位，再向左平移2个单位，分别得到点A，B的对应点C，D，连接AC，BD，AB．
（1）求点C，D的坐标及四边形ABDC的面积S四边形ABCD；
（2）在y轴上是否存在一点M，连接MC，MD，使S△MCD＝
S四边形ABCD？若存在这样一点，求出点M的坐标，若不存在，试说明理由；
（3）点P是直线BD上的一个动点，连接PA，PO，当点P在BD上移动时（不与B，D重合），直接写出∠BAP，∠DOP，∠APO之间满足的数量关系．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
