
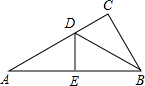
 如图,在Rt△ABC中,∠C=90°,BD平分∠ABC,交AC于D,沿DE所在直线折叠,使点B恰好与点A重合,若CD=3,AB=8,则DB的值为5.
如图,在Rt△ABC中,∠C=90°,BD平分∠ABC,交AC于D,沿DE所在直线折叠,使点B恰好与点A重合,若CD=3,AB=8,则DB的值为5. 分析 由角平分线可得∠CBD=∠EBD,由折叠可得∠A=∠EDB,进而求得∠A=∠CBD=30°,利用直角三角形中30°锐角所对的直角边等于斜边的一半,进而可求出BC的长,再利用勾股定理即可求出DB的长.
解答 解:∵BD平分∠ABC,
∴∠CBD=∠EBD,
∵沿DE所在直线折叠,使点B恰好与点A重合,
∴DE⊥AB,∠A=∠DBA,
∴∠DBC=∠A=∠DBA=30°,
∴AB=2BC,
∵AB=8,
∴BC=4,
∵CD=3,
∴DB=$\sqrt{C{D}^{2}+B{C}^{2}}$=5.
故答案为:5.
点评 此题考查了折叠的性质、勾股定理的运用以及角平分线、含30°角的直角三角形的性质,得到30°的角是正确解答本题的关键.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
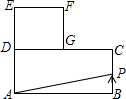 如图,已知长方形ABCD中,AB=4,BC=2,正方形DEFG的边长为2,且点G在CD上,动点P从点B出发,以1个单位长度/s的速度沿折线B→C→G→F向终点F运动,设运动时间为xs,△PAB的面积为y,则y与x之间的函数关系用图象可以表示为( )
如图,已知长方形ABCD中,AB=4,BC=2,正方形DEFG的边长为2,且点G在CD上,动点P从点B出发,以1个单位长度/s的速度沿折线B→C→G→F向终点F运动,设运动时间为xs,△PAB的面积为y,则y与x之间的函数关系用图象可以表示为( )| A. |  | B. | 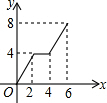 | C. | 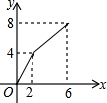 | D. | 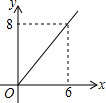 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
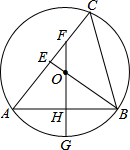 如图,△ABC内接于⊙O,B0的延长线交AC于E,过O作FG⊥AB,交AC于F,交AB于H,交⊙O于G.⊙O的半径为12,且OE:OF:OB=2:3:6,则弧BG的长为( )
如图,△ABC内接于⊙O,B0的延长线交AC于E,过O作FG⊥AB,交AC于F,交AB于H,交⊙O于G.⊙O的半径为12,且OE:OF:OB=2:3:6,则弧BG的长为( )| A. | 4$\sqrt{3}$π | B. | 4$\sqrt{2}$π | C. | 2$\sqrt{3}$π | D. | 4π |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,ABCD是矩形纸片,翻折∠B、∠D,使BC、AD恰好落在AC上.设F、H分别是B、D落在AC上的点,E、G分别是折痕CE与AB、AG与CD的交点.
如图,ABCD是矩形纸片,翻折∠B、∠D,使BC、AD恰好落在AC上.设F、H分别是B、D落在AC上的点,E、G分别是折痕CE与AB、AG与CD的交点. 查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (1)先化简,再求值:(3a2-ab+7)-(5ab-4a2+7),其中a=2,b=$\frac{1}{3}$.
(1)先化简,再求值:(3a2-ab+7)-(5ab-4a2+7),其中a=2,b=$\frac{1}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,12根火柴棒排成一个“井”字形,要求移动图中的4根火柴棒,使原图形变成三个相同的正方形,且没有火柴棒剩余(同一根火柴棒只能移动一次),你有什么好办法?试试看,画出移动后的图形,并标明移动前后的火柴棒.
如图,12根火柴棒排成一个“井”字形,要求移动图中的4根火柴棒,使原图形变成三个相同的正方形,且没有火柴棒剩余(同一根火柴棒只能移动一次),你有什么好办法?试试看,画出移动后的图形,并标明移动前后的火柴棒.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
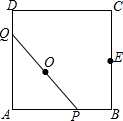 如图,正方形ABCD的边长是4,E是BC的中点,动点P、Q在正方形ABCD的边上运动,且PQ=4.若点P从点A出发,沿A→B→E的线路,向点E运动,相应的,点Q在DA,AB上运动.则点P从A到E的运动过程中,PQ的中点O所经过的路线长等于$\frac{4π}{3}$.
如图,正方形ABCD的边长是4,E是BC的中点,动点P、Q在正方形ABCD的边上运动,且PQ=4.若点P从点A出发,沿A→B→E的线路,向点E运动,相应的,点Q在DA,AB上运动.则点P从A到E的运动过程中,PQ的中点O所经过的路线长等于$\frac{4π}{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com