
 如图,△ABC中,BD、CE分别是AC、AB上的中线,BD与CE相交于点O,点M、N分别是OB、OC的中点,连接DE、EM、MN、ND.
如图,△ABC中,BD、CE分别是AC、AB上的中线,BD与CE相交于点O,点M、N分别是OB、OC的中点,连接DE、EM、MN、ND.分析 (1)由中位线定理,可得ED∥BC,MN∥BC,且都等于边长BC的一半.分析到此,此题证明即可.
(2)作BC边上的中线AF,交BD于G,连接DF,作FH⊥AC于HAP⊥BC于P.想办法求出AF即可解决问题;
解答 (1)证明:∵BD、CE分别是AC、AB上的中线,
∴点E为线段AB的中点,点D为线段AC的中点,
∴DE为△ABC的中位线,
∴DE∥BC,且BC=2DE.
∵点M、N分别是OB、OC的中点,
∴MN为△OBC的中位线,
∴MN∥BC,且BC=2MN.
∴DE∥MN,DE=MN,
∴四边形DEMN是平行四边形,
(2)作BC边上的中线AF,交BD于G,连接DF,作FH⊥AC于HAP⊥BC于P.
∵BD、AF是边AC、BC上的中线,
∴DF∥BA,DF=$\frac{1}{2}$BA.
∴△DOF∽△BOA,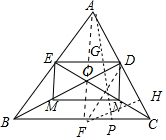
∴$\frac{OD}{OB}$=$\frac{1}{2}$,
即BD=3DO,
∵四边形DEMN是菱形,且BC=4cm,AC=6cm,
∴EM=DN=MN=2cm,
∴OA=4,OF=3,AF=6,
易知AF=AC=6.PF=PC=1,AP=$\sqrt{35}$,
FH=$\frac{CF•AP}{AC}$=$\frac{\sqrt{35}}{3}$,CH=$\frac{1}{3}$,DH=$\frac{8}{3}$,DF=$\sqrt{F{H}^{2}+D{H}^{2}}$=$\sqrt{11}$,
∴AB=2DF=2$\sqrt{11}$.
点评 此题主要考查了平行四边形的判定,三角形的中位线定理,关键是掌握三角形的中位线平行于第三边,并且等于第三边的一半.


 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:解答题
 已知如图,在△ABC中,BE、CF分别是AC、AB边上的高,在BE的延长线上截取BM=AC,在CF的延长线上截取CN=AB,请说明:
已知如图,在△ABC中,BE、CF分别是AC、AB边上的高,在BE的延长线上截取BM=AC,在CF的延长线上截取CN=AB,请说明:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 册数 | 0 | 1 | 2 | 3 | 4册及以上 |
| 人数 | 3 | 13 | 16 | a | 5 |
| A. | 13 | B. | 16 | C. | 104 | D. | 128 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
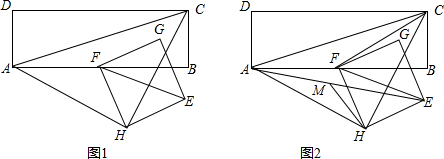
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
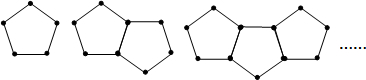
| A. | 33 | B. | 32 | C. | 31 | D. | 30 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com