
如图,等边△ABC的边长为4,E是边BC上的动点,EH⊥AC于H,过E作EF∥AC,交线段AB于点F,在线段AC上取点P,使PE=EB.设EC=x(0<x≤2).

(1)请直接写出图中与线段EF相等的两条线段(不再另外添加辅助线);
(2)Q是线段AC上的动点,当四边形EFPQ是平行四边形时,求平行四边形EFPQ的面积(用含 的代数式表示);
的代数式表示);
(3)当(2)中 的平行四边形EFPQ面积最大值时,以E为圆心,r为半径作圆,根据⊙E与此时平行四边形EFPQ四条边交点的总个数,求相应的r的取值范围.
(1)BE、PE;
(2)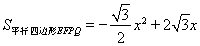 ;
;
(3)当⊙E与平行四边形EFPQ的四条边交点的总个数是2个时,0<r<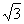 ;
;
当⊙E与平行四边形EFPQ的四条边交点的总个数是4个时,r=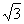 ;??
;??
当⊙E与平行四边形EFPQ的四条边交点的总个数是6个时,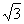 <r<2;
<r<2;
当⊙E与平行四边形EFPQ的四条边交点的总个数是3个时,r=2;
当⊙E与平行四边形EFPQ的四条边交点的总个数是0个时,r>2.
【解析】
试题分析:(1)根据三角形ABC是等边三角形和EF∥AC,可得等边三角形BEF,则可写出与EF相等的线段;
(2)根据(1)可知EF=BE=4﹣x,要求平行四边形的面积,只需求得EF边上的高.作EH⊥AC于H,根据30度的直角三角形EHC进行表示EH的长,进一步求得平行四边形的面积;
(3)根据二次函数的顶点式或顶点的公式法求得平行四边形的面积的最大值时x的值,分析平行四边形的位置和形状.然后根据公共点的个数分析圆和平行四边形的各边的位置关系,进一步根据圆和直线的位置关系求得r的取值范围.
试题解析:(1)BE、PE、BF三条线段中任选两条;
(2)作EQ∥FP交FE于E,
设EC为x
∵EH⊥AC,
∴∠EHC=90°
∴△CHE为直角三角形
∵△ABC为等边三角形,
∴∠C=60°
在Rt△CHE中,∠CHE=90°,∠C=60°,
∠HEC=180°﹣∠C﹣∠EHC=30°
∴2HC=EC
∵HE2=EC2﹣HC2
∴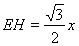 ,
,
∵EF∥AC,FP∥EQ
∴四边形EFPQ为平行四边形
∴PQ=FE
又∵PE=BE
∴PQ=EF=BE=4﹣x
∴ ;
;

(3)因为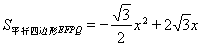
 ,所以当x=2时,平行四边形EFPQ的面积最大.此时E、F、P分别为△ABC的三边BC、AB、AC的中点,且C、Q重合,四边形EFPQ是边长为2的菱形(如图).
,所以当x=2时,平行四边形EFPQ的面积最大.此时E、F、P分别为△ABC的三边BC、AB、AC的中点,且C、Q重合,四边形EFPQ是边长为2的菱形(如图).
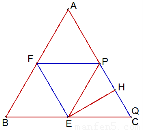
过点E点作ED⊥FP于D,则ED=EH=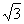 .
.
当⊙E与平行四边形EFPQ的四条边交点的总个数是2个时,0<r<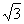 ;
;
当⊙E与平行四边形EFPQ的四条边交点的总个数是4个时,r=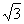 ;??
;??
当⊙E与平行四边形EFPQ的四条边交点的总个数是6个时,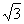 <r<2;
<r<2;
当⊙E与平行四边形EFPQ的四条边交点的总个数是3个时,r=2;
当⊙E与平行四边形EFPQ的四条边交点的总个数是0个时,r>2.
考点:二次函数综合题.


 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:
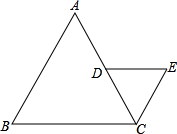 如图,等边△ABC的边长为l,取边AC的中点D,在外部画出一个新的等边三角形△CDE,如此绕点C顺时针继续下去,直到所画等边三角形的一边与△ABC的BC边重叠为止,此时这个三角形的边长为
如图,等边△ABC的边长为l,取边AC的中点D,在外部画出一个新的等边三角形△CDE,如此绕点C顺时针继续下去,直到所画等边三角形的一边与△ABC的BC边重叠为止,此时这个三角形的边长为查看答案和解析>>
科目:初中数学 来源: 题型:
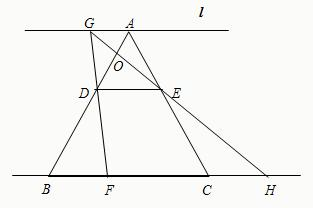 已知:如图,等边△ABC的边长为6,点D、E分别在AB、AC上,且AD=AE=2,直线l过点A,且l∥BC,若点F从点B开始以每秒1个单位长的速度沿射线BC方向运动,设F点运动的时间为t秒,当t>0时,直线DF交l于点G,GE的延长线与BC的延长线交于点H,AB与GH相交于点O.
已知:如图,等边△ABC的边长为6,点D、E分别在AB、AC上,且AD=AE=2,直线l过点A,且l∥BC,若点F从点B开始以每秒1个单位长的速度沿射线BC方向运动,设F点运动的时间为t秒,当t>0时,直线DF交l于点G,GE的延长线与BC的延长线交于点H,AB与GH相交于点O.查看答案和解析>>
科目:初中数学 来源: 题型:
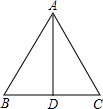 如图,等边△ABC的边长为2,AD是△ABC的角平分线,
如图,等边△ABC的边长为2,AD是△ABC的角平分线,查看答案和解析>>
科目:初中数学 来源: 题型:
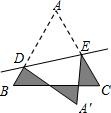 如图,等边△ABC的边长为1cm,D、E分别是AB、AC上的点,将△ADE沿直线DE折叠,点A落在点A′处,且点A′在△ABC外部,则阴影部分图形的周长为( )
如图,等边△ABC的边长为1cm,D、E分别是AB、AC上的点,将△ADE沿直线DE折叠,点A落在点A′处,且点A′在△ABC外部,则阴影部分图形的周长为( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com