
 ,AF=1,求EM的长.
,AF=1,求EM的长.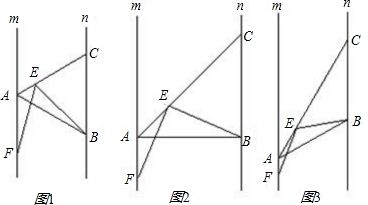
 ,
, ,即BG=
,即BG= AE;
AE; AE.
AE. AE,即AE=
AE,即AE= ;
; ;
; ,
, ,ME=MF;
,ME=MF; ×(4-
×(4- )=
)= ,解得ME=
,解得ME= .
.
 :1,因此结论应该是BC=
:1,因此结论应该是BC= AE+AF.
AE+AF. AE,进而可根据BC、AF的长得到AE的值;在Rt△AFE中,易求得FG=AE=
AE,进而可根据BC、AF的长得到AE的值;在Rt△AFE中,易求得FG=AE= ,那么可证得△AEM≌△GFM,即可得到AM=MG,且ME=FM,因此只需求得FM即可.由(1)(2)的解答过程可知A、F、B、E四点共圆,在这个圆中,利用相交弦定理即可求得ME的值.
,那么可证得△AEM≌△GFM,即可得到AM=MG,且ME=FM,因此只需求得FM即可.由(1)(2)的解答过程可知A、F、B、E四点共圆,在这个圆中,利用相交弦定理即可求得ME的值.

 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:初中数学 来源: 题型:
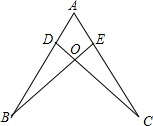 如图,已知:点D、E分别是AB、AC上的点,线段CD与线段BE相交于点O,且DB=EC=2AD,DC=BE,问:点E是线段AC的几等分点,并给出证明.
如图,已知:点D、E分别是AB、AC上的点,线段CD与线段BE相交于点O,且DB=EC=2AD,DC=BE,问:点E是线段AC的几等分点,并给出证明.查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |
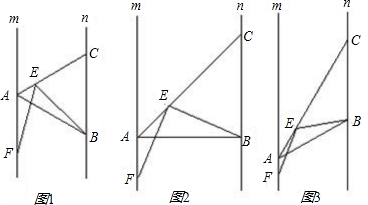
查看答案和解析>>
科目:初中数学 来源: 题型:
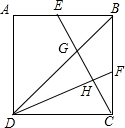 如图,已知:点E、F分别是正方形ABCD的边AB、BC的中点,BD、DF分别交CE于点G、H,若正方形ABCD的面积是240,则四边形BFHG的面积等于( )
如图,已知:点E、F分别是正方形ABCD的边AB、BC的中点,BD、DF分别交CE于点G、H,若正方形ABCD的面积是240,则四边形BFHG的面积等于( )| A、26 | B、28 | C、24 | D、30 |
查看答案和解析>>
科目:初中数学 来源: 题型:
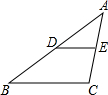 如图,证明定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半.
如图,证明定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半.| 1 | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com