
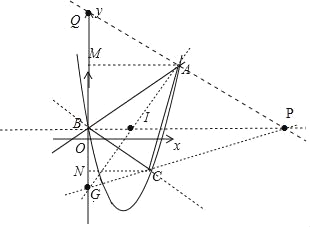
【题目】已知一次函数y=x+1与抛物线y=x2+bx+c交A(m,9),B(0,1)两点,点C在抛物线上且横坐标为6.
(1)写出抛物线的函数表达式;
(2)判断△ABC的形状,并证明你的结论;
(3)平面内是否存在点Q在直线AB、BC、AC距离相等,如果存在,请直接写出所有符合条件的Q的坐标,如果不存在,说说你的理由.

【答案】(1)y=x2﹣7x+1;(2)△ABC为直角三角形.理由见解析;(3)符合条件的Q的坐标为(4,1),(24,1),(0,﹣7),(0,13).
【解析】
(1)先利用一次函数解析式得到A(8,9),然后利用待定系数法求抛物线解析式;
(2)先利用抛物线解析式确定C(6,﹣5),作AM⊥y轴于M,CN⊥y轴于N,如图,证明△ABM和△BNC都是等腰直角三角形得到∠MBA=45°,∠NBC=45°,AB=8![]() ,BN=6
,BN=6![]() ,从而得到∠ABC=90°,所以△ABC为直角三角形;
,从而得到∠ABC=90°,所以△ABC为直角三角形;
(3)利用勾股定理计算出AC=10![]() ,根据直角三角形内切圆半径的计算公式得到Rt△ABC的内切圆的半径=2
,根据直角三角形内切圆半径的计算公式得到Rt△ABC的内切圆的半径=2![]() ,设△ABC的内心为I,过A作AI的垂线交直线BI于P,交y轴于Q,AI交y轴于G,如图,则AI、BI为角平分线,BI⊥y轴,PQ为△ABC的外角平分线,易得y轴为△ABC的外角平分线,根据角平分线的性质可判断点P、I、Q、G到直线AB、BC、AC距离相等,由于BI=
,设△ABC的内心为I,过A作AI的垂线交直线BI于P,交y轴于Q,AI交y轴于G,如图,则AI、BI为角平分线,BI⊥y轴,PQ为△ABC的外角平分线,易得y轴为△ABC的外角平分线,根据角平分线的性质可判断点P、I、Q、G到直线AB、BC、AC距离相等,由于BI=![]() ×2
×2![]() =4,则I(4,1),接着利用待定系数法求出直线AI的解析式为y=2x﹣7,直线AP的解析式为y=﹣
=4,则I(4,1),接着利用待定系数法求出直线AI的解析式为y=2x﹣7,直线AP的解析式为y=﹣![]() x+13,然后分别求出P、Q、G的坐标即可.
x+13,然后分别求出P、Q、G的坐标即可.
(1)把A(m,9)代入y=x+1得m+1=9,解得m=8,则A(8,9),
把A(8,9),B(0,1)代入y=x2+bx+c得![]() ,解得
,解得![]() ,
,
∴抛物线解析式为y=x2﹣7x+1;
故答案为y=x2﹣7x+1;
(2)△ABC为直角三角形.理由如下:
当x=6时,y=x2﹣7x+1=36﹣42+1=﹣5,则C(6,﹣5),
作AM⊥y轴于M,CN⊥y轴于N,如图,
∵B(0,1),A(8,9),C(6,﹣5),
∴BM=AM=8,BN=CN=6,
∴△ABM和△BNC都是等腰直角三角形,
∴∠MBA=45°,∠NBC=45°,AB=8![]() ,BN=6
,BN=6![]() ,
,
∴∠ABC=90°,
∴△ABC为直角三角形;
(3)∵AB=8![]() ,BN=6
,BN=6![]() ,
,
∴AC=10![]() ,
,
∴Rt△ABC的内切圆的半径=![]() ,
,
设△ABC的内心为I,过A作AI的垂线交直线BI于P,交y轴于Q,AI交y轴于G,如图,
∵I为△ABC的内心,
∴AI、BI为角平分线,
∴BI⊥y轴,
而AI⊥PQ,
∴PQ为△ABC的外角平分线,
易得y轴为△ABC的外角平分线,
∴点I、P、Q、G为△ABC的内角平分线或外角平分线的交点,
它们到直线AB、BC、AC距离相等,
BI=![]() ×2
×2![]() =4,
=4,
而BI⊥y轴,
∴I(4,1),
设直线AI的解析式为y=kx+n,
则![]() ,解得
,解得![]() ,
,
∴直线AI的解析式为y=2x﹣7,
当x=0时,y=2x﹣7=﹣7,则G(0,﹣7);
设直线AP的解析式为y=﹣![]() x+p,
x+p,
把A(8,9)代入得﹣4+n=9,解得n=13,
∴直线AP的解析式为y=﹣![]() x+13,
x+13,
当y=1时,﹣![]() x+13=1,则P(24,1)
x+13=1,则P(24,1)
当x=0时,y=﹣![]() x+13=13,则Q(0,13),
x+13=13,则Q(0,13),
综上所述,符合条件的Q的坐标为(4,1),(24,1),(0,﹣7),(0,13).


 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:
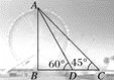
【题目】某校数学兴趣小组要测量摩天轮的高度.如图,他们在C处测得摩天轮的最高点A的仰角为45°,再往摩天轮的方向前进50 m至D处,测得最高点A的仰角为60°.问摩天轮的高度AB约是( )
(结果精确到1 米,参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
A. 120米 B. 117米 C. 118米 D. 119米
查看答案和解析>>
科目:初中数学 来源: 题型:
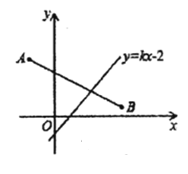
【题目】如图,在平面直角坐标系中,线段AB的端点坐标为A(-2,4),B(4,2),直线y=kx-2与线段AB有交点,则K的值不可能是( )
A. -5B. -2C. 3D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实验数据显示,一般成人喝半斤低度白酒后,1.5时内其血液中酒精含量y(毫克/百毫升)与时间![]() (时)的关系可近似地用二次函数
(时)的关系可近似地用二次函数![]() 刻画;1.5时后(包括1.5时)y与x可近似地用反比例函数
刻画;1.5时后(包括1.5时)y与x可近似地用反比例函数![]() (k>0)刻画(如图所示).
(k>0)刻画(如图所示).
(1)根据上述数学模型计算:
①喝酒后几时血液中的酒精含量达到最大值?最大值为多少?
②当![]() =5时,y=45.求k的值.
=5时,y=45.求k的值.
(2)按国家规定,车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升时属于“酒后驾驶”,不能驾车上路.参照上述数学模型,假设某驾驶员晚上20:00在家喝完半斤低度白酒,第二天早上7:00能否驾车去上班?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
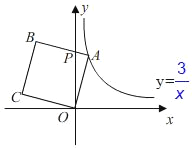
【题目】如图,点A在反比例函数y=![]() (x>0)上,以OA为边作正方形OABC,边AB交y轴于点P,若PA:PB=1:2,则正方形OABC的面积=_____.
(x>0)上,以OA为边作正方形OABC,边AB交y轴于点P,若PA:PB=1:2,则正方形OABC的面积=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,AD是高,E、F分别是AB、AC的中点,
中,AD是高,E、F分别是AB、AC的中点,
(1)AB=10,AC=8,求四边形AEDF的周长;
(2)EF与AD有怎样的位置关系,证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小宇在周日上午8:00从家出发,乘车1小时到达某活动中心参加实践活动.11:00时他在活动中心
接到爸爸的电话,因急事要求他在12:00前回到家,他即刻按照来活动中心时的路线,以5千米/时的平均速
度快步返回.同时,爸爸从家沿同一路线开车接他,在距家20千米处接上了小宇,立即保持原来的车速原
路返回.设小宇离家 x 小时后,到达离家y千米的地方,图中折线OABCD表示 y 与 x 之间的函数关系.下
列叙述错误的是( )
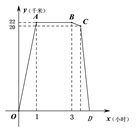
A. 活动中心与小宇家相距22千米
B. 小宇在活动中心活动时间为2小时
C. 他从活动中心返家时,步行用了0.4小时
D. 小宇不能在12:00前回到家
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AD>AB.

(1)作出∠ABC的平分线(尺规作图,保留作图痕迹,不写作法);
(2)若(1)中所作的角平分线交AD于点E,AF⊥BE,垂足为点O,交BC于点F,连接EF.求证:四边形ABFE为菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,我国海监船在钓鱼岛附近的O处观测到一可疑船正匀速直线航行我国海域,当该可疑船位于点O的北偏东30°方向上的点A处(OA=20![]() km)时,我方开始向对方喊话,但该可疑船仍匀速航行,40min后,又测得该可疑船位于点O的正北方向上的点B处,且OB=20km,求该可疑船航行的速度.
km)时,我方开始向对方喊话,但该可疑船仍匀速航行,40min后,又测得该可疑船位于点O的正北方向上的点B处,且OB=20km,求该可疑船航行的速度.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com