
如图,在直角梯形纸片ABCD中,AD∥BC,∠A=90°,∠C=30°,点F是CD边上一点,将纸片沿BF折叠,点C落在E点,使直线BE经过点D,若BF=CF=8,则AD的长为 .
【解析】
试题分析:利用等边对等角可以得到∠FBC=∠C=30°,再利用折叠的性质可以得到∠EBF=∠CBF=30°,从而可以求得∠BDF的度数,即可以求得线段BD,然后在直角三角形ABD中求解即可.
∵BF=CF=8,
∴∠FBC=∠C=30°,
∵折叠纸片使BC经过点D,点C落在点E处,BF是折痕,
∴∠EBF=∠CBF=30°,
∴∠EBC=60°,
∴∠BDF=90°
∵∠EBC=60°
∴∠ADB=60°,
∵BF=CF=8.
∴BD=BF?sin60°=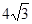
∴在Rt△BAD中,AD=BD×sin30°=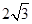 .
.
考点:梯形,矩形、直角三角形的相关知识
点评:解决此类题要懂得用梯形的常用辅助线,把梯形分割为矩形和直角三角形,从而由矩形和直角三角形的性质来求解.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:初中数学 来源: 题型:
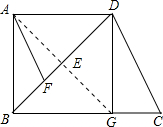 如图,在直角梯形纸片ABCD中,AD∥BC,∠ABC=90°,将纸片沿过点A的直线折叠,使点B与点D重合,折痕为AG.连接DG并展开纸片.
如图,在直角梯形纸片ABCD中,AD∥BC,∠ABC=90°,将纸片沿过点A的直线折叠,使点B与点D重合,折痕为AG.连接DG并展开纸片.| 1 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在直角梯形纸片ABCD中,AD∥BC,∠A=90°,∠C=30°,点F是CD边上的一点,将纸片沿BF折叠,点C落在E点,使直线BE经过点D,若BF=CF=8,则AD的长为
如图,在直角梯形纸片ABCD中,AD∥BC,∠A=90°,∠C=30°,点F是CD边上的一点,将纸片沿BF折叠,点C落在E点,使直线BE经过点D,若BF=CF=8,则AD的长为| 3 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在直角梯形纸片ABCD中,AB∥DC,∠A=90°,CD>AD,将纸片沿过点D的直线折叠,使点A落在边CD上的点E处,折痕为DF.连接EF并展开纸片.
如图,在直角梯形纸片ABCD中,AB∥DC,∠A=90°,CD>AD,将纸片沿过点D的直线折叠,使点A落在边CD上的点E处,折痕为DF.连接EF并展开纸片.查看答案和解析>>
科目:初中数学 来源:2013届上海市虹口区中考二模数学试卷(带解析) 题型:填空题
如图,在直角梯形纸片ABCD中,AD∥BC,∠A=90°,∠C=30°,点F是CD边上一点,将纸片沿BF折叠,点C落在E点,使直线BE经过点D,若BF=CF=8,则AD的长为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com