
 如图,在□ABCD中,点E、F分别在边AD、AB上,∠BCF=∠DCE.
如图,在□ABCD中,点E、F分别在边AD、AB上,∠BCF=∠DCE.分析 (1)直接利用平行四边形的性质结合相似三角形的判定方法得出答案;
(2)利用相似三角形的性质结合平行四边形的性质得出答案.
解答 解:(1)△BCF与△DCE相似,
理由:∵四边形ABCD是平行四边形,
∴∠B=∠D,
又∵∠BCF=∠DCE,
∴△BCF∽△DCE;
(2)∵△BCF∽△DCE,
∴$\frac{BC}{DC}$=$\frac{BF}{DE}$,
∵AB=10,AD=6,E是AD的中点,
∴DE=3,BC=6,DC=10,
∴$\frac{6}{10}$=$\frac{BF}{3}$,
解得:BF=1.8.
点评 此题主要考查了相似三角形的判定与性质,正确掌握相似三角形的判定与性质是解题关键.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案科目:初中数学 来源: 题型:解答题
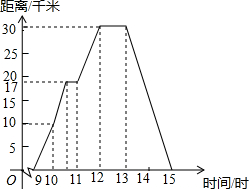 小明某天上午9时骑自行车离开家,15时回家,他描绘了离家的距离与时间的变化情况.
小明某天上午9时骑自行车离开家,15时回家,他描绘了离家的距离与时间的变化情况.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 △ABC三个顶点的坐标分别为A (2,7),B (6,8),C (8,2),请你分别完成下面的作图并标出所有顶点的坐标.
△ABC三个顶点的坐标分别为A (2,7),B (6,8),C (8,2),请你分别完成下面的作图并标出所有顶点的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
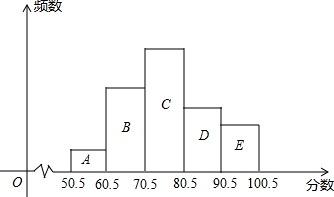 从某校参加科普知识竞赛的学生试卷中,抽取一个样本了解竞赛成绩的分布情况,将样本分成A、B、C、D、E五个组,绘制成如图所示的频数分布直方图,图中A、B、C、D、E各小组的长方形的高的比是l:4:6:3:2,且A组的频数是5,请结合直方图提供的信息,解答下列问题.
从某校参加科普知识竞赛的学生试卷中,抽取一个样本了解竞赛成绩的分布情况,将样本分成A、B、C、D、E五个组,绘制成如图所示的频数分布直方图,图中A、B、C、D、E各小组的长方形的高的比是l:4:6:3:2,且A组的频数是5,请结合直方图提供的信息,解答下列问题.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,二次函数y=-x2+mx+3的图象与y轴交于点A,与x轴的负半轴交于点B,且△AOB的面积为6.
如图,二次函数y=-x2+mx+3的图象与y轴交于点A,与x轴的负半轴交于点B,且△AOB的面积为6.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com