
如下图,n+1个腰长为2的等腰直角三角形斜边在同一直线上,设△B2D1C1(阴影部分)的面积为S1,△B3D2C2的面积为S2,…,△Bn+1DnCn的面积为Sn,则S2=__________;Sn=__________.(用含n的式子表示).

1,
【解析】
试题分析:
解:∵n+1个边长为2的等腰三角形有一条边在同一直线上,
∴S△AB1C1= ×2=1,
×2=1,
连接B1、B2、B3、B4、B5点,显然它们共线且平行于AC1
∵∠B1C1B2=90°
∴A1B1∥B2C1
∴△B1C1B2是等腰直角三角形,且边长=2,
∴△B1B2D1∽△C1AD1,
∴B1D1:D1C1=1:1,
∴S1= ×2 =1 ,
×2 =1 ,
故答案为:1 ;
同理:B2B3:AC2=1:2,
∴B2D2:D2C2=1:2,
∴S2= ×2 =
×2 = ,
,
同理:B3B4:AC3=1:3,
∴B3D3:D3C3=1:3,
∴S3= ×2=
×2= ,
,
∴S4= ×2=
×2= ,
…
,
…
∴Sn=
考点:1.相似三角形的判定与性质;2.三角形的面积;3.等腰直角三角形.


 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案科目:初中数学 来源: 题型:
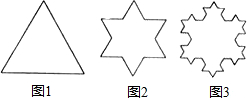 长应等于( )
长应等于( )| A、3 | ||
B、
| ||
C、
| ||
D、
|
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2004年全国中考数学试题汇编《代数式》(01)(解析版) 题型:选择题




查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com