
【题目】已知抛物线![]() 经过点
经过点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 是该抛物线上一点,且在第四象限内,连接
是该抛物线上一点,且在第四象限内,连接![]() .
.
(1)求抛物线的函数解析式,并写出对称轴;
(2)当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
(3)在(2)的条件下,如果点![]() 是
是![]() 轴上一点,点
轴上一点,点![]() 是抛物线上一点,当以点
是抛物线上一点,当以点![]() 为顶点的四边形是平行四边形时,请直接写出点
为顶点的四边形是平行四边形时,请直接写出点![]() 的坐标.
的坐标.
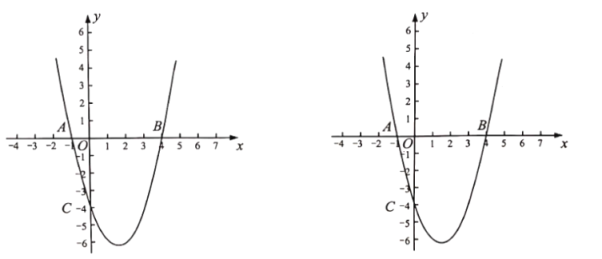
【答案】(1)![]() ,对称轴为直线
,对称轴为直线![]() ; (2)
; (2)![]() ;(3)点
;(3)点![]() 的坐标为
的坐标为![]() 或
或![]() 或
或![]() 或
或![]() .
.
【解析】
(1)根据点A,B的坐标,利用待定系数法可求出抛物线的解析式,即可写出对称轴;
(2)连接![]() ,求出C点坐标,根据A、B、C点坐标求出
,求出C点坐标,根据A、B、C点坐标求出![]() ,设
,设![]() ,
,
根据![]() ,列出关于x的方程,解方程即可求出D点坐标;
,列出关于x的方程,解方程即可求出D点坐标;
(3)分两种情形:如图2中,当AE为平行四边形的边时,根据DF=AE=1,求解即可.如图3中,当AE,DF是平行四边形的对角线时,根据点F的纵坐标为6,求出点F的坐标,再根据中点坐标公式求解即可.
(1)∵![]() 经过点
经过点![]() ,
,
![]() ,
,
![]() ,
,
∴抛物线的解析式为![]() ,
,
对称轴为直线![]() .
.
(2)连接![]() ,
,
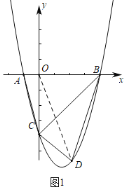
∵抛物线![]() 经过点
经过点![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
又![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
设![]() ,
,
∵点![]() 在第四象限,
在第四象限,
![]() ,
,
![]()
=![]()
=![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
(3)如图2中,当AE为平行四边形的边时,
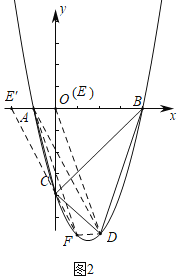
∵DF∥AE,D(2,-6)
∴F(1,-6),
∴DF=1,
∴AE=1,
∴E(0,0),或E′(-2,0).
如图3中,当AE,DF是平行四边形的对角线时,
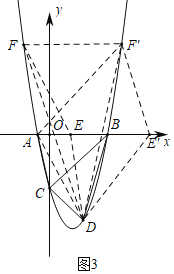
∵点D与点F到x轴的距离相等,
∴点F的纵坐标为6,
当y=6时,6=x2-3x-4,
解得x=-2或5,
∴F(-2,6)或(5,6),
设E(n,0),则有![]() 或
或![]() ,
,
解得n=1或8,
∴E(1,0)或(8,0),
综上所述,满足条件的点E的坐标为(0,0)或(1,0)或(8,0)或(-2,0).


科目:初中数学 来源: 题型:
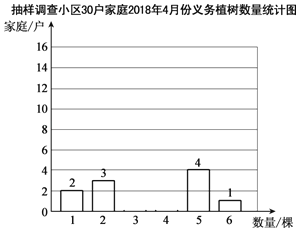
【题目】“绿水青山就是金山银山”,北京市民积极参与义务植树活动.小武同学为了了解自己小区300户家庭在2018年4月份义务植树的数量,进行了抽样调查,随即抽取了其中30户家庭,收集的数据如下(单位:棵):
1 1 2 3 2 3 2 3 3 4 3 3 4 3 3
5 3 4 3 4 4 5 4 5 3 4 3 4 5 6
(1)对以上数据进行整理、描述和
①绘制如下的统计图,请补充完整;
②这30户家庭2018年4月份义务植树数量的平均数是______,众数是______;
(2)“互联网+全民义务植树”是新时代首都全民义务植树组织形式和尽责方式的一大创新,2018年首次推出义务植树网上预约服务,小武同学所调查的这30户家庭中有7户家庭采用了网上预约义务植树这种方式,由此可以估计该小区采用这种形式的家庭有______户.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司推出一款产品,经市场调查发现,该产品的日销售量y(个)与销售单价x(元)之间满足一次函数关系.关于销售单价,日销售量,日销售利润的几组对应值如下表:
销售单价x(元) | 85 | 95 | 105 | 115 |
日销售量y(个) | 175 | 125 | 75 | m |
日销售利润w(元) | 875 | 1875 | 1875 | 875 |
(注:日销售利润=日销售量×(销售单价﹣成本单价))
(1)求y关于x的函数解析式(不要求写出x的取值范围)及m的值;
(2)根据以上信息,填空:
该产品的成本单价是 元,当销售单价x= 元时,日销售利润w最大,最大值是 元;
(3)公司计划开展科技创新,以降低该产品的成本,预计在今后的销售中,日销售量与销售单价仍存在(1)中的关系.若想实现销售单价为90元时,日销售利润不低于3750元的销售目标,该产品的成本单价应不超过多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在△ABC中,∠ACB=90°,∠B=30°,AC=1,D为AB的中点,EF为△ACD 的中位线,四边形EFGH为△ACD的内接矩形(矩形的四个顶点均在△ACD的边上).
(1)计算矩形EFGH的面积;
(2)将矩形EFGH沿AB向右平移,F落在BC上时停止移动.在平移过程中,当矩形与△CBD重叠部分的面积为![]() 时,求矩形平移的距离;
时,求矩形平移的距离;
(3)如图③,将(2)中矩形平移停止时所得的矩形记为矩形![]() ,将矩形
,将矩形![]() 绕
绕![]() 点按顺时针方向旋转,当
点按顺时针方向旋转,当![]() 落在CD上时停止转动,旋转后的矩形记为矩形
落在CD上时停止转动,旋转后的矩形记为矩形![]() ,设旋转角为
,设旋转角为![]() ,求
,求![]() 的值.
的值.
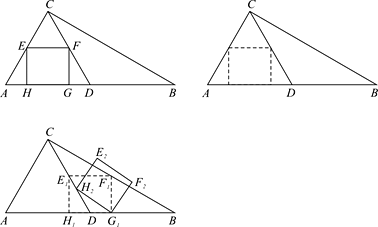
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,以
,以![]() 为边在直线左下方作菱形
为边在直线左下方作菱形![]() ,且点
,且点![]() 在
在![]() 轴负半轴上,点
轴负半轴上,点![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() ,以
,以![]() ,
,![]() 为邻边构造矩形
为邻边构造矩形![]() ,
,![]() 交
交![]() 轴的正半轴于点
轴的正半轴于点![]() .
.
(1)求证:![]() ;
;
(2)当![]() 时,
时,
①求![]() 的长,
的长,
②在菱形![]() 的边上取一点
的边上取一点![]() ,在矩形
,在矩形![]() 的边上取一点
的边上取一点![]() ,若以
,若以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形,求出所有满足条件的
为顶点的四边形是平行四边形,求出所有满足条件的![]() 点的坐标.
点的坐标.
(3)连结![]() ,记
,记![]() 的面积为
的面积为![]() ,
,![]() 的面积为
的面积为![]() ,若
,若![]() ,求
,求![]() 的值
的值
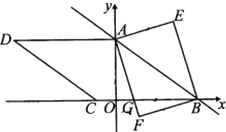
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90o,BE是它的角平分线,D在AB边上,以DB为直径的半圆O经过点E.
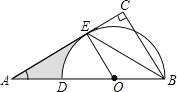
(1)试说明:AC是圆O的切线;
(2)若∠A=30o,圆O的半径为4,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解市民“获取新闻的最主要途径”,某市记者开展了一次抽样调查,要求被调查的市民必选且只能选一项.根据调查结果绘制了如图尚不完整的扇形统计图,其中将“手机上网”和“电脑上网”作为“获取新闻的最主要途径”的市民分别有600人和510人,并且扇形统计图中![]() ,
,![]() 满足
满足![]() .请根据所给信息,解答下列问题:
.请根据所给信息,解答下列问题:

(1)请计算扇形统计图中“电脑上网”所在扇形的圆心角的度数;
(2)求扇形统计图中![]() ,
,![]() 的值;
的值;
(3)若该市约有200万人,请你估计其中将“手机上网”和“报纸”作为“获取新闻的最主要途径”的总人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 过点A(﹣3,0),B(﹣2,3),C(0,3),其顶点为D.
过点A(﹣3,0),B(﹣2,3),C(0,3),其顶点为D.
(1)求抛物线的解析式;
(2)设点M(1,m),当MB+MD的值最小时,求m的值;
(3)若P是抛物线上位于直线AC上方的一个动点,求△APC的面积的最大值;
(4)若抛物线的对称轴与直线AC相交于点N,E为直线AC上任意一点,过点E作EF∥ND交抛物线于点F,以N,D,E,F为顶点的四边形能否为平行四边形?若能,求点E的坐标;若不能,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com