练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    △ABC≌△AB′C′，其中∠A′=35°，∠B=70°，则∠C的度数为


    1. A.
      55°
    2. B.
      60°
    3. C.
      70°
    4. D.
      75°
    D
    分析：根据两三角形全等可得两个三角形的对应角相等，即∠A′=∠A，∠B=∠B′，∠C=∠C′，已知两角的度数，再根据三角形内角和度数即可得∠C的度数．
    解答：∵△ABC≌△AB′C′，
    ∴∠A′=∠A，∠B=∠B′，∠C=∠C′，
    已知∠A′=35°，∠B=70°，
    ∴∠C=180°-∠A-∠B=180°-35°-70°=75°．
    故选D．
    点评：本题考查了全等三角形的性质和三角形内角和定理，熟练掌握全等三角形的性质是解此题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    （2005•乌兰察布）如图，已知AC平分∠PAQ，点B，B′分别在边AP，AQ上．下列条件中不能推出AB=AB′的是（　　）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，点C是∠PAQ的平分线上一点，点B、B′分别在边AP、AQ上，如果再添加一个条件，即可推出AB=AB′，那么该条件不可以是（　　）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （2010•保定一模）如图，A、B、C分别表示面积为9、10、11的三个圆．已知三个圆所覆盖的总面积为20．A与B、B与C、C与A每两圆公共部分所覆盖面积分别为5、4、3，求A、B、C三个圆公共部分所覆盖的面积．

    探索发现：
    我们把三个圆所覆盖的总面积记为A∨B∨C；每两圆公共部分所覆盖的面积记为AB、BC、CA；三个圆公共部分所覆盖的面积记为ABC．根据题意，有：
    （1）三个圆的面积和为：A+B+C=
    30
    30
    ；
    （2）重合部分覆盖的面积为（A+B+C）-A∨B∨C=
    10
    10
    ；
    （3）每两圆公告部分所覆盖的面积和为：AB+BC+CA=
    12
    12
    ；
    （4）三个圆公共部分所覆盖的面积：ABC=
    2
    2
    ．
    总结归纳：
    利用上题中规定的符号和解答过程，补全等式：ABC=
    AB+BC+CA+A∨B∨C-（A+B+C）
    AB+BC+CA+A∨B∨C-（A+B+C）
    ．
    利用上述方法得到的启示，解决下面的问题：
    某年级共有74名学生参加课外小组．其中，参加球类的有34人，参加棋类的有32人，参加田径类的有30人；既参加球类又参加棋类的有7人，既参加棋类又参加田径类的有8人，既参加田径类又参加球类的有10人．求三个小组都参加的人数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知AC平分∠PAQ，点B、B′分别在边AP、AQ上，如果添加一个条件，即可推出AB=AB′，下列条件中哪个可能无法推出AB=AB′（　　）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

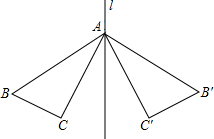    如图，△ABC和△AB′C′关于直线l对称，下列结论：
    （1）∠ABC≌△AB′C′；
    （2）∠BAC′=∠B′AC；
    （3）l垂直平分CC′；
    （4）直线BC和B′C′的交点不一定在l上．
    其中正确的有（　　）

    查看答案和解析>>

    同步练习册答案