
【题目】阅读并探究下列问题:

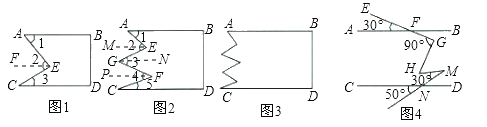
(1)如图1,将长方形纸片剪两刀,其中AB∥CD,则∠2与∠1、∠3有何关系?为什么?
(2)如图2,将长方形纸片剪四刀,其中AB∥CD,则∠2+∠4与∠1+∠3+∠5有何关系?为什么?
(3)如图3,将长方形纸片剪n刀,其中AB∥CD,你又有何发现?
(4)如图4,直线AB∥CD,∠EFA=30°,∠FGH=90°,∠HMN=30°,∠CNP=50°,则∠GHM= .
【答案】(1)∠2=∠1+∠3;(2)∠2+∠4=∠1+∠3+∠5;(3)开口向左的角的度数的各等于开口向右的角的度数的和;(4)40°.
【解析】
(1)过E点作EF∥AB,则EF∥CD,根据两直线平行,内错角相等得到∠AEF=∠1,∠CEF=∠3,即有∠2=∠1+∠3;
(2)分别过E、G、F分别作EM∥AB,GN∥AB,FP∥AB,根据两直线平行,内错角相等,同(1)一样易得到∠2+∠4=∠1+∠3+∠5;
(3)综合(1)(2)易得开口向左的角的度数的各等于开口向右的角的度数的和.
(4)利用(3)的结论得到∠BFG+∠GHM+∠MND=∠FGH+∠HMN,易计算出∠GHM.
(1)图1中,∠2=∠1+∠3.理由如下:
过E点作EF∥AB,如图,
则EF∥CD,
∴∠AEF=∠1,∠CEF=∠3,
∴∠2=∠1+∠3
(2)图2中,分别过E、G、F分别作EM∥AB,GN∥AB,FP∥AB,
同(1)的证明方法一样可得∠2+∠4=∠1+∠3+∠5;
(3)图3中,开口向左的角的度数的各等于开口向右的角的度数的和.
(4)图4中,由(3)的结论得,∠BFG+∠GHM+∠MND=∠FGH+∠HMN,
∴30°+∠GHM+50°=90°+30°,
∴∠GHM=40°.
故答案为40°.


 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:初中数学 来源: 题型:
【题目】某次考试中,某班级的数学成绩统计图如图.下列说法错误的是( )

A. 得分在70~80分之间的人数最多 B. 该班的总人数为40
C. 得分在90~100分之间的人数最少 D. 及格(≥60分)人数是26
查看答案和解析>>
科目:初中数学 来源: 题型:
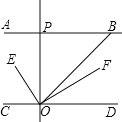
【题目】AB∥CD,OE平分∠BOC,OF⊥OE,OP⊥CD,∠ABO=a°.则下列结论: ①∠BOE=![]() (180﹣a)°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.其中正确结论__________(填编号).
(180﹣a)°;②OF平分∠BOD;③∠POE=∠BOF;④∠POB=2∠DOF.其中正确结论__________(填编号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,点D为△ABC内的一点,∠ADB=120°,∠ADC=90°,将△ABD绕点A逆时针旋转60°得△ACE,连接DE.
(1)求证:AD=DE;
(2)求∠DCE的度数;
(3)若BD=1,求AD,CD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】任何一个正整数n都可以进行这样的分解:n=s×t(s,t是正整数,且s≤t),如果p×q在n的所有这种分解中两因数之差的绝对值最小,我们就称p×q是n的最佳分解,并规定:F(n)=![]() .例如18可分解成1×18,2×9,3×6这三种,这时就有F(18)=
.例如18可分解成1×18,2×9,3×6这三种,这时就有F(18)=![]() =
=![]() .给出下列关于F(n)的说法:
.给出下列关于F(n)的说法:
(1)F(2)=![]() ;(2)F(12)=
;(2)F(12)=![]() ;(3)F(27)=3;(4)若n是一个完全平方数,则F(n)=1.
;(3)F(27)=3;(4)若n是一个完全平方数,则F(n)=1.
其中正确说法的个数是( )
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,下列能判定AB∥CD的条件有( )个.
(1)∠B+∠BCD=180°;(2)∠1=∠2;(3)∠3=∠4;(4)∠B=∠5.

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上A、B两点分别对应有理数a、b,A、B两点之间的距离表示为AB,在数轴上A、B两点之间的距离AB=|a﹣b|,利用数形结合思想回答下列问题:
![]()
(1)数轴上表示2和10两点之间的距离是 ,数轴上表示2和﹣10两点之间的距离是 ;
(2)数轴上,x和﹣2两点之间的距离是 ;
(3)若x表示一个有理数,则|x﹣1|+|x+2|有最小值吗?若有,请求出最小值,若没有,写出理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里装有只有颜色不同的黑、白两种球共40个,小李做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是实验中的一组统计数据:

(1)请估计:当实验次数为5000次时,摸到白球的频率将会接近 ;(精确到0.1)
(2)假如你摸一次,你摸到白球的概率P(摸到白球)= ;
(3)试验估算这个不透明的盒子里黑球有多少只?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个汽车零件制造车间可以生产甲,乙两种零件,生产4个甲种零件和3个乙种零件共获利120元;生产2个甲种零件和5个乙种零件共获利130元.
(1)求生产1个甲种零件,1个乙种零件分别获利多少元?
(2)若该汽车零件制造车间共有工人30名,每名工人每天可生产甲种零件6个或乙种零件5个,每名工人每天只能生产同一种零件,要使该车间每天生产的两种零件所获总利润超过2800元,至少要派多少名工人去生产乙种零件?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com