
 ИзНјЈ¬ЕЧОпПЯy=-$\frac{1}{2}$x2+mx+nУлxЦбҪ»УЪAЎўBБҪөгЈ¬УлyЦбҪ»УЪөгCЈ¬ЕЧОпПЯөД¶ФіЖЦбҪ»xЦбУЪөгDЈ¬ТСЦӘAЈЁ-1Ј¬0Ј©Ј¬CЈЁ0Ј¬2Ј©Ј®
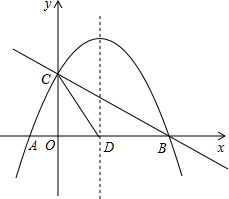
ИзНјЈ¬ЕЧОпПЯy=-$\frac{1}{2}$x2+mx+nУлxЦбҪ»УЪAЎўBБҪөгЈ¬УлyЦбҪ»УЪөгCЈ¬ЕЧОпПЯөД¶ФіЖЦбҪ»xЦбУЪөгDЈ¬ТСЦӘAЈЁ-1Ј¬0Ј©Ј¬CЈЁ0Ј¬2Ј©Ј®·ЦОц ЈЁ1Ј©АыУГҙэ¶ЁПөКэ·ЁЗуЕЧОпПЯөДұнҙпКҪЈ»
ЈЁ2Ј©ТФCDОӘСьөДөИСьИэҪЗРОУРИэёцЈәўЩўЪТФDОӘФІРДЈ¬ТФCDОӘ°лҫ¶»ӯ»ЎҪ»¶ФіЖЦбУЪP1ЎўP2Ј¬ўЫТФCОӘФІРДЈ¬ТФCDОӘ°лҫ¶»ӯ»ЎЈ¬Ҫ»¶ФіЖЦбУЪP3Ј¬·ЦұрЗуіцХвИэёцөгөДЧшұкЈ»
ЈЁ3Ј©ПИёщҫЭ¶ФіЖРФЗуөгBөДЧшұкОӘЈЁ4Ј¬0Ј©Ј¬ФЩЗуЦұПЯBCөДҪвОцКҪЈ¬ЙиіцөгEәНFөДЧшұкЈ¬ұнКҫEFөДіӨЈ»ФтЛДұЯРОBDCFөДГж»эөИУЪБҪёцИэҪЗРОГж»эөДәНЈ¬ЖдЦРЎчBDCКЗ¶ЁЦөЈ¬ЎчBFCөДГж»э=ЗҰЦұёЯ¶ИУлЛ®ЖҪҝн¶ИөД»эЈ¬ҙъИлГж»э№«КҪҝЙЗуөГSөДҪвОцКҪЈ¬ЗуЧоЦөјҙҝЙЈ®
Ҫвҙр 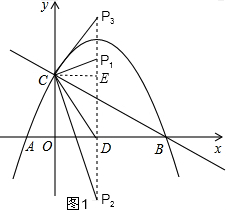 ҪвЈәЈЁ1Ј©°СAЈЁ-1Ј¬0Ј©Ј¬CЈЁ0Ј¬2Ј©ҙъИлy=-$\frac{1}{2}$x2+mx+nЦРөГЈә
ҪвЈәЈЁ1Ј©°СAЈЁ-1Ј¬0Ј©Ј¬CЈЁ0Ј¬2Ј©ҙъИлy=-$\frac{1}{2}$x2+mx+nЦРөГЈә
$\left\{\begin{array}{l}{0=-\frac{1}{2}-m+n}\\{2=n}\end{array}\right.$Ј¬
ҪвөГЈә$\left\{\begin{array}{l}{m=\frac{3}{2}}\\{n=2}\end{array}\right.$Ј¬
ЎаЕЧОпПЯөДұнҙпКҪОӘЈә$y=-\frac{1}{2}{x^2}+\frac{3}{2}x+2$Ј»
ЈЁ2Ј©$y=-\frac{1}{2}{x^2}+\frac{3}{2}x+2$=-$\frac{1}{2}$ЈЁx-$\frac{3}{2}$Ј©2+$\frac{25}{8}$Ј»
ЎаDЈЁ$\frac{3}{2}$Ј¬0Ј©Ј¬
ФЪRtЎчOCDЦРЈ¬OC=2Ј¬OD=$\frac{3}{2}$Ј¬
УЙ№ҙ№Й¶ЁАнөГЈәCD=$\sqrt{{2}^{2}+ЈЁ\frac{3}{2}Ј©^{2}}$=$\frac{5}{2}$Ј¬
ўЩөұCD=DP1КұЈ¬ЎчPCDКЗөИСьИэҪЗРОЈ¬
ЎаP1ЈЁ$\frac{3}{2}$Ј¬$\frac{5}{2}$Ј©Ј¬
ўЪөұCD=DP2КұЈ¬ЎчPCDКЗөИСьИэҪЗРОЈ¬
ЎаP2ЈЁ$\frac{3}{2}$Ј¬-$\frac{5}{2}$Ј©Ј¬
ўЫөұCD=CP3КұЈ¬ЎчPCDКЗөИСьИэҪЗРОЈ¬
№эCЧчCEЎНDP1УЪEЈ¬
ЎЯCЈЁ0Ј¬2Ј©Ј¬
ЎаDE=OC=2Ј¬
ЎЯCD=CP3Ј¬
ЎаDE=P3E=2Ј¬
ЎаP3ЈЁ$\frac{3}{2}$Ј¬4Ј©Ј¬
ЧЫЙПЛщКцЈ¬PөгөДЧшұкОӘЈәP1ЈЁ$\frac{3}{2}$Ј¬$\frac{5}{2}$Ј©Ј¬P2ЈЁ$\frac{3}{2}$Ј¬-$\frac{5}{2}$Ј©Ј¬P3ЈЁ$\frac{3}{2}$Ј¬4Ј©Ј»
ЈЁ3Ј©ИзНј2Ј¬
ЎЯAЈЁ-1Ј¬0Ј©Ј¬¶ФіЖЦбКЗЈәx=$\frac{3}{2}$Ј¬
ЎаBЈЁ4Ј¬0Ј©Ј¬
ЙиBCөДҪвОцКҪОӘЈәy=kx+bЈ¬
°СBЈЁ4Ј¬0Ј©Ј¬CЈЁ0Ј¬2Ј©ҙъИлөГЈә$\left\{\begin{array}{l}{4k+b=0}\\{b=2}\end{array}\right.$Ј¬
ҪвөГЈә$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=2}\end{array}\right.$Ј¬
ЎаBCөДҪвОцКҪОӘЈәy=-$\frac{1}{2}$x+2Ј¬
ЙиE$ЈЁmЈ¬-\frac{1}{2}m+2Ј©$Ј¬FЈЁ$mЈ¬-\frac{1}{2}{m^2}+\frac{3}{2}m+2Ј©$Ј¬
ЎаEF=-$\frac{1}{2}{m}^{2}+\frac{3}{2}m+2$-ЈЁ-$\frac{1}{2}$m+2Ј©=-$\frac{1}{2}{m}^{2}$+2mЈ¬
ЎаSЛДұЯРОBDCF=SЎчBCD+SЎчBFC=$\frac{1}{2}$BD•OC+$\frac{1}{2}$EF•OB=$\frac{1}{2}$ЎБ$\frac{5}{2}$ЎБ2+$\frac{1}{2}$ЈЁ-$\frac{1}{2}{m}^{2}$+2mЈ©ЎБ4Ј¬
S=-m2+4m+2.5Ј¬
=-ЈЁm-2Ј©2+6.5ЈЁ0ЈјmЈј4Ј©Ј¬
өұm=2КұЈ¬-$\frac{1}{2}$m+2=-$\frac{1}{2}$ЎБ2+2=1Ј¬
Ўаөұm=2КұЈ¬ЛДұЯРОCDBFөДГж»эЧоҙуЈ¬ЧоҙуОӘ6.5Ј¬ҙЛКұEЈЁ2Ј¬1Ј©Ј®
өгЖА ұҫМвКЗ¶юҙОәҜКэөДЧЫәПМвЈ¬ҝјІйБЛАыУГҙэ¶ЁПөКэ·ЁЗу¶юҙОәҜКэәНТ»ҙОәҜКэөДҪвОцКҪЈ¬өЪ¶юОК№№ҪЁөИСьИэҪЗРОКұІЙУГ·ЦАаМЦВЫөДЛјПлЈ¬ө«ТӘЧўТвКЗ№№ҪЁТФCDОӘСьөДөИСьИэҪЗРОЈ»ФЪөЪИэОКЦРЈ¬И·¶ЁЛДұЯРОГж»эөДЧоҙуЦөКұЈ¬ФЛУГГж»эәНЗуЛДұЯРОөДГж»эЈ¬Н¬Кұ»№АыУГБЛәҜКэөДҪвОцКҪұнКҫөгөДЧшұкЈ¬ХвФЪәҜКэМвЦРҫӯіЈФЛУГЈ¬ТӘКмБ·ХЖОХЈ®



| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈәМоҝХМв
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈәҪвҙрМв
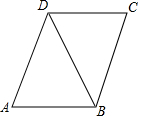 ИзНјЈ¬ТСЦӘAB=CDЈ¬AD=CBЈ¬ЗуЦӨЈәЎчABDЎХЎчCDBЈ®
ИзНјЈ¬ТСЦӘAB=CDЈ¬AD=CBЈ¬ЗуЦӨЈәЎчABDЎХЎчCDBЈ®Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈәҪвҙрМв
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈәҪвҙрМв
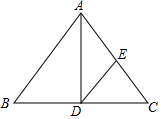 ИзНјЈ¬ADКЗөИСьИэҪЗРОABCөДөЧұЯBCЙПөДёЯЈ¬DEЎОABЈ¬Ҫ»ACУЪөгEЈ®ЗуЦӨЎчAEDКЗөИСьИэҪЗРОЈ®
ИзНјЈ¬ADКЗөИСьИэҪЗРОABCөДөЧұЯBCЙПөДёЯЈ¬DEЎОABЈ¬Ҫ»ACУЪөгEЈ®ЗуЦӨЎчAEDКЗөИСьИэҪЗРОЈ®Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈәСЎФсМв
 ТСЦӘ¶юҙОәҜКэy=ax2+bx+cЈЁaЎЩ0Ј©өДНјПуИзНјЛщКҫЈ¬ЗТ№ШУЪxөДТ»ФӘ¶юҙО·ҪіМax2+bx+c-m=0Г»УРКөКэёщЈ¬УРПВБРҪбВЫЈәўЩabcЈј0Ј»ўЪb2-4acЈҫ0Ј»ўЫmЈҫ2Ј»ўЬөұxЈј0КұЈ¬yЛжxөДФцҙу¶шФцҙуЈ®ЖдЦРХэИ·ҪбВЫөДёцКэКЗЈЁЎЎЎЎЈ©
ТСЦӘ¶юҙОәҜКэy=ax2+bx+cЈЁaЎЩ0Ј©өДНјПуИзНјЛщКҫЈ¬ЗТ№ШУЪxөДТ»ФӘ¶юҙО·ҪіМax2+bx+c-m=0Г»УРКөКэёщЈ¬УРПВБРҪбВЫЈәўЩabcЈј0Ј»ўЪb2-4acЈҫ0Ј»ўЫmЈҫ2Ј»ўЬөұxЈј0КұЈ¬yЛжxөДФцҙу¶шФцҙуЈ®ЖдЦРХэИ·ҪбВЫөДёцКэКЗЈЁЎЎЎЎЈ©| AЈ® | 4 | BЈ® | 3 | CЈ® | 2 | DЈ® | 1 |
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈәМоҝХМв

Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәіхЦРКэС§ АҙФҙЈә МвРНЈәҪвҙрМв
Ійҝҙҙр°ёәНҪвОц>>
°Щ¶ИЦВРЕ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com