
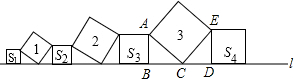
分析 如图,易证△CDE≌△ABC,得AB2+DE2=DE2+CD2=CE2,同理FG2+LK2=HL2,S1+S2+S3+S4=1+3=4.
解答 解:在△CDE和△ABC中,
$\left\{\begin{array}{l}{∠EDC=∠CBA}\\{∠ECD=∠CAB}\\{EC=CA}\end{array}\right.$,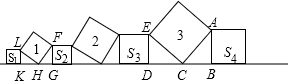
∴△CDE≌△ABC(AAS),
∴AB=CD,BC=DE,
∴AB2+DE2=DE2+CD2=CE2=3,
同理可证FG2+LK2=HL2=1,
∴S1+S2+S3+S4=CE2+HL2=1+3=4.
点评 本题考查了全等三角形的证明,考查了勾股定理的灵活运用,本题中证明AB2+DE2=DE2+CD2=CE2是解题的关键.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:初中数学 来源: 题型:解答题
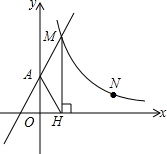 如图,直线y=2x+2与y轴交于A点,与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=2.
如图,直线y=2x+2与y轴交于A点,与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x<$\frac{m}{3}$ | B. | x<-$\frac{m}{4}$ | C. | x<-$\frac{m}{3}$ | D. | x<$\frac{m}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系,A(a,0),B(b,0),C(-1,2),且|2a+b+1|+(a+2b-4)2=0.
如图,在平面直角坐标系,A(a,0),B(b,0),C(-1,2),且|2a+b+1|+(a+2b-4)2=0.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图1是手机放在手机支架上,其侧面示意图如图2所示,AB,CD是长度不变的活动片,一端A固定在0A上,另一端B可在0C上变动位置,若将AB变到AB′的位置,则0C旋转一定角度到达0C′的位置.已知0A=8cm,AB⊥0C,∠B0A=60°,sin∠B′A0=$\frac{9}{10}$,则点B′到0A的距离为( )
如图1是手机放在手机支架上,其侧面示意图如图2所示,AB,CD是长度不变的活动片,一端A固定在0A上,另一端B可在0C上变动位置,若将AB变到AB′的位置,则0C旋转一定角度到达0C′的位置.已知0A=8cm,AB⊥0C,∠B0A=60°,sin∠B′A0=$\frac{9}{10}$,则点B′到0A的距离为( )| A. | $\frac{9\sqrt{3}}{10}$cm | B. | $\frac{18\sqrt{3}}{10}$cm | C. | $\frac{9\sqrt{3}}{5}$cm | D. | $\frac{18\sqrt{3}}{5}$cm |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
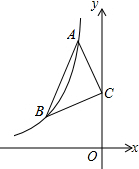 如图:已知点A、B是反比例函数y=-$\frac{6}{x}$上在第二象限内的分支上的两个点,点C(0,3),且△ABC满足AC=BC,∠ACB=90°,则线段AB的长为2$\sqrt{5}$.
如图:已知点A、B是反比例函数y=-$\frac{6}{x}$上在第二象限内的分支上的两个点,点C(0,3),且△ABC满足AC=BC,∠ACB=90°,则线段AB的长为2$\sqrt{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
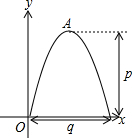 如图,一抛物线桥拱的最高点A到水面的距离为p,在水面上截得的距离为q,如图所示,建立平面直角坐标系.
如图,一抛物线桥拱的最高点A到水面的距离为p,在水面上截得的距离为q,如图所示,建立平面直角坐标系.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com