
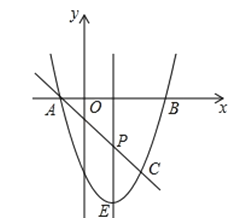
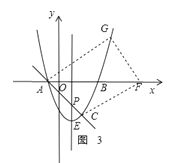
【题目】如图,抛物线y=ax2+bx﹣3与x轴交于A,B两点(A点在B点左侧),A(﹣1,0),B(3,0),直线l与抛物线交于A,C两点,其中C点的横坐标为2.
(1)求抛物线的函数解析式;
(2)P是线段AC上的一个动点,过P点作y轴的平行线交抛物线于E点,求线段PE长度的最大值;
(3)点G是抛物线上的动点,在x轴上是否存在点F,使A,C,F,G这样的四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的F点坐标;如果不存在,请说明理由.
【答案】(1)y=x2﹣2x﹣3;(2)![]() ;(3)F1(1,0),F2(﹣3,0),F3(
;(3)F1(1,0),F2(﹣3,0),F3(![]() ,0),F4(
,0),F4(![]() ,0).
,0).
【解析】
(1)利用待定系数法,直接求出抛物线的解析式即可;
(2)根据点C在抛物线上,求出点C的坐标;根据待定系数法求出直线AC的解析式;设点P的横坐标为x(1≤x≤2),则P、E的坐标分别为P(x,x1),E(x,x22x3),用含x的式子表示出PE的长度,求出PE的最大值;
(3)根据点G的不同位置,分为4种情况讨论,点G在第二象限的抛物线上,点G在抛物线与y轴的交点上(两种情况),点G在直线AC上方y轴右侧,根据平行四边形的对边平行且相等,求得点F的坐标即可.
(1)∵抛物线y=ax2+bx﹣3与x轴交于A(﹣1,0),B(3,0),
∴![]() ,解得:
,解得:![]() ,∴抛物线的函数解析式为:y=x2﹣2x﹣3;
,∴抛物线的函数解析式为:y=x2﹣2x﹣3;
(2)∵点C在抛物线上,且点C的横坐标为2,
∴y=4﹣4﹣3=﹣3,
∴点C的坐标为(2,﹣3),
设直线AC的解析式为:y=kx+b,
∴![]() ,解得:
,解得:![]() ,
,
∴直线AC的解析式为:y=﹣x﹣1,设点P的横坐标为x(﹣1≤x≤2),
则P、E的坐标分别为P(x,﹣x﹣1),E(x,x2﹣2x﹣3).
∵点P在点E的上方,
∴PE=(﹣x﹣1)﹣(x2﹣2x﹣3)=﹣x2+x+2=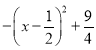 .
.
∵﹣1<0,开口向下,﹣1≤x≤2,
∴当x=![]() 时,PE最大=
时,PE最大=![]() ;
;
(3)存在4个这样的点F,分别是F1(1,0),F2(﹣3,0),F3(4+![]() ,0),F4(4﹣
,0),F4(4﹣![]() ,0).
,0).
∵A,C,F,G这样的四个点为顶点的四边形是平行四边形
①如图1,四边形AFGC是平行四边形,此时CG∥AF,
∴AF=CG=2,
∴点F的坐标为(﹣3,0);
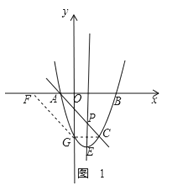
②如图2,四边形AGCF是平行四边形,此时CG∥FA,
∴AF=CG=2.
∵点A的坐标为(﹣1,0),
∴点F的坐标为(1,0);
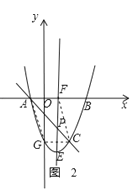
③如图3,四边形ACFG时平行四边形,此时AC∥GF,
此时点C,G两点的纵坐标互为相反数,
故点G的纵坐标为3,且点G在抛物线上,
∴x2﹣2x﹣3=3,
解得:x1=1+![]() ,x2=1﹣
,x2=1﹣![]() (舍去),
(舍去),
∴点G的坐标为(1+![]() ,3).
,3).
∵GF∥AC,
∴设直线GF的解析式为:y=﹣x+h,
∴﹣(1+![]() )+h=3,
)+h=3,
解得:h=4+![]() ,
,
∴直线GH的解析式为:y=﹣x+4+![]() ,
,
∴直线GF与x轴的交点F的坐标为(4+![]() ,0);
,0);
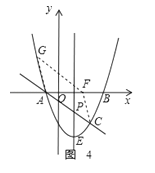
④如图4,同③可求得点F的坐标为(4﹣![]() ,0).
,0).
综上所述:存在4个这样的点F,分别是F1(1,0),F2(﹣3,0),F3(4+![]() ,0),F4(4﹣
,0),F4(4﹣![]() ,0).
,0).


科目:初中数学 来源: 题型:
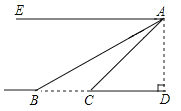
【题目】如图,为测量某条河的宽度BC,工程队用无人机在距地面高度为200米的A处测得B,C两点的俯角分别为30°和45°,且点B,C,D在同一水平直线上,求A,C之间的距离和这条河的宽度BC.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,射线
,射线![]() 从与射线
从与射线![]() 重合的位置开始,绕点
重合的位置开始,绕点![]() 按顺时针方向旋转,与射线
按顺时针方向旋转,与射线![]() 重合时就停止旋转,射线
重合时就停止旋转,射线![]() 与线段
与线段![]() 相交于点
相交于点![]() ,点
,点![]() 是线段
是线段![]() 的中点.
的中点.
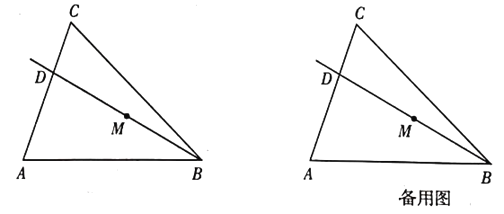
(1)求线段![]() 的长;
的长;
(2)①当点![]() 与点
与点![]() 、点
、点![]() 不重合时,过点
不重合时,过点![]() 作
作![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() ,在射线
,在射线![]() 旋转的过程中,
旋转的过程中,![]() 的大小是否发生变化?若不变,求
的大小是否发生变化?若不变,求![]() 的度数;若变化,请说明理由.
的度数;若变化,请说明理由.
②在①的条件下,连接![]() ,直接写出
,直接写出![]() 面积的最小值____________.
面积的最小值____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
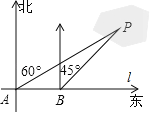
【题目】为了计算湖中小岛上凉亭P到岸边公路l的距离,某数学兴趣小组在公路l上的点A处,测得凉亭P在北偏东60°的方向上;从A处向正东方向行走200米,到达公路l上的点B处,再次测得凉亭P在北偏东45°的方向上,如图所示.求凉亭P到公路l的距离.(结果保留整数,参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
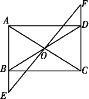
【题目】如图所示,在矩形ABCD中,O是AC与BD的交点,过点O的直线EF与AB,CD的延长线分别交于点E,F.
(1)求证:△BOE≌△DOF;
(2)当EF与AC满足什么条件时,四边形AECF是菱形?并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,并解答后面的问题.
在学习了直角三角形的边角关系后,小颖和小明两个学习小组继续探究任意锐角三角形的边角关系:在锐角△ABC中,∠A、∠B、∠C的对边分别是a、b、c.
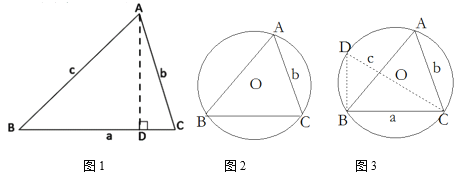
(1)小明学习小组发现如下结论:
如图1,过A作AD⊥BC于D,则sinB=![]() ,sinC=
,sinC=![]() 即AD=csinB,AD=bsinC,于是_____=______即
即AD=csinB,AD=bsinC,于是_____=______即![]() ,同理有
,同理有![]() ,
,![]()
则有![]()
(2)小颖学习小组则利用圆的有关性质也得到了类似的结论:
如图2,△ABC的外接圆半径为R,连结CO并延长交⊙O于点D,连结DB,则∠D=∠A,
∵CD为⊙O的直径,∴∠DBC=90°,
在Rt△DBC中,
∵![]() ,
,
∴![]() ,
,![]()
同理:![]() ,
,
则有![]()
请你将这一结论用文字语言描述出来: .
小颖学习小组在证明过程中略去了“![]() ”的证明过程,请你把“
”的证明过程,请你把“![]() ”的证明过程补写出来.
”的证明过程补写出来.
(3)直接用前面阅读材料中得出的结论解决问题
规划局为了方便居民,计划在三个住宅小区A、B、C之间修建一座学校,使它到三个住宅小区的距离相等,已知小区C在小区B的正东方向![]() 千米处,小区A在小区B的东北方向,且A与C之间相距
千米处,小区A在小区B的东北方向,且A与C之间相距![]() 千米,求学校到三个小区的距离及小区A在小区C的什么方向?
千米,求学校到三个小区的距离及小区A在小区C的什么方向?
查看答案和解析>>
科目:初中数学 来源: 题型:
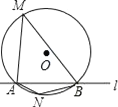
【题目】如图,⊙O的半径是2,直线l与⊙O相交于A、B两点,M、N是⊙O上的两个动点,且在直线l的异侧,若∠AMB=45°,则四边形MANB面积的最大值是( )
A. 2![]() B. 4 C. 4
B. 4 C. 4![]() D. 8
D. 8![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某物业公司计划对所管理的小区3000m2区域进行绿化,经投标由甲、乙两个工程队来完成,甲、乙两个工程队每天共完成绿化面积150m2,甲队完成600m2区域的绿化面积与乙队完成300m2区域的绿化面积所用的天数相同.
(1)求甲、乙两个工程队每天各能完成多少面积的绿化?
(2)若甲队每天绿化费用是0.6万元,乙队每天绿化费用是0.2万元,该物业公司要使这次绿化总费用不超过17万元,则至少安排乙工程队绿化多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“端午节”是我国的传统佳节,民间历来有吃“粽子”的习俗.我市某食品厂为了解市民对去年销量较好的肉馅粽、豆沙馅粽、红枣馅粽、蛋黄馅粽(以下分别用A,B,C,D表示)这四种不同口味粽子的喜爱情况,在节前对某居民区市民进行了抽样调查,并将调查情况绘制成如下两幅统计图(尚不完整).
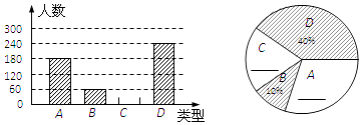
请根据以上信息回答:
(1)将两幅不完整的图补充完整;
(2)本次参加抽样调查的居民有多少人?
(3)若居民区有8000人,请估计爱吃D粽的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com