
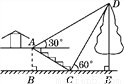
如图,小叶与小高欲测量公园内某棵树DE的高度.他们在这棵树正前方的一座楼亭前的台阶上的点A处测得这棵树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处,测得这棵树顶端D的仰角为60°.已知点A的高度AB为3 m,台阶AC的坡度为1∶ ,且B,C,E三点在同一条直线上,那么这棵树DE的高度为( )
,且B,C,E三点在同一条直线上,那么这棵树DE的高度为( )
A. 6 m B. 7 m C. 8 m D. 9 m
D 【解析】过点A作AF⊥DE于点F,则四边形ABEF为矩形, ∴AF=BE,EF=AB=3m. 设DE=xm,在Rt△CDE中,CE==xm. 在Rt△ABC中,∵=,AB=3m, ∴BC=3m. 在Rt△AFD中,DF=DE-EF=(x-3) m, ∴AF== (x-3) m. ∵AF=BE=BC+CE, ∴ (x-3)=3+x, 解...科目:初中数学 来源:广东省东莞市翰林学校2017-2018学年八年级(上)期中数学试卷(word版含答案解析) 题型:单选题
如图所示的一块地,已知∠ADC=90°,AD=12m,CD=9m,AB=25m,BC=20m,则这块地的面积为( )平方米.

A. 96 B. 204 C. 196 D. 304
A 【解析】连接AC,运用勾股定理逆定理可证△ACD,△ABC为直角三角形,可求出两直角三角形的面积,此块地的面积为两个直角三角形的面积差. 【解析】 连接AC, 则在Rt△ADC中, AC2=CD2+AD2=122+92=225, ∴AC=15,在△ABC中,AB2=1521, AC2+BC2=152+362=1521, ∴AB2=AC2+BC2, ∴∠ACB=90...查看答案和解析>>
科目:初中数学 来源:2018人教版八年级数学下册练习:第十九章达标检测卷 题型:填空题
甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步600米,先到终点的人原地休息.已知甲先出发2秒.在跑步过程中,甲、乙两人的距离y(米)与乙出发的时间t(秒)之间的关系如图所示,则b=_____.

查看答案和解析>>
科目:初中数学 来源:2018人教版九年级数学下册练习:第二十八章 达标检测卷 题型:解答题
某水库大坝的横截面是如图所示的四边形ABCD,其中AB∥CD.大坝顶上有一瞭望台PC,PC正前方有两艘渔船M,N.观察员在瞭望台顶端P处观测到渔船M的俯角α为31°,渔船N的俯角β为45°.已知MN所在直线与PC所在直线垂直,垂足为E,且PE长为30米.
(1)求两渔船M,N之间的距离(结果精确到1米).
(2)已知坝高24米,坝长100米,背水坡AD的坡度i=1∶0.25.为提高大坝防洪能力,请施工队将大坝的背水坡通过填筑土石方进行加固,坝底BA加宽后变为BH,加固后背水坡DH的坡度i=1∶1.75.施工队施工10天后,为尽快完成加固任务,施工队增加了机械设备.工作效率提高到原来的2倍,结果比原计划提前20天完成加固任务,施工队原计划平均每天填筑土石方多少立方米?
(参考数据:tan 31°≈0.60,sin 31°≈0.52)

查看答案和解析>>
科目:初中数学 来源:2018人教版九年级数学下册练习:第二十八章 达标检测卷 题型:解答题
计算:(1)2sin 30°+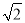 cos 45°-
cos 45°- tan 60°;(2)tan230°+cos230°-sin245°tan 45°.
tan 60°;(2)tan230°+cos230°-sin245°tan 45°.
查看答案和解析>>
科目:初中数学 来源:2018人教版九年级数学下册练习:第二十八章 达标检测卷 题型:单选题
如图,在平面直角坐标系中,P是第一象限内的点,其坐标是(3,m),且OP与x轴正半轴的夹角α的正切值是 ,则sinα的值是( )
,则sinα的值是( )

A. 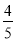 B.
B.  C.
C.  D.
D. 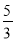
查看答案和解析>>
科目:初中数学 来源:河南省周口市西华县2017-2018学年八年级上学期期末考试数学试卷 题型:解答题
某超市用5 000元资金购进一批新品种的苹果进行试销,由于试销状况良好,超市又调拨了11 000元资金购进该种苹果,但这次的进价比试销时每千克多了0.5元,购进苹果的数量是试销时的2倍.
(1)试销时该品种苹果的进价是每千克多少元?
(2)如果超市将该品种苹果按每千克7元定价出售,当大部分苹果售出后,余下的400千克按定价的七折售完,那么超市在这两次苹果销售中共盈利多少元?
(1)试销时该品种苹果的进价是5元/千克;(2)超市在两次苹果销售中盈利4160元 【解析】试题分析:(1)设试销时苹果的进货价是x元/斤,根据“11000元购进该种苹果的进货价比试销时多了0.5元,购进苹果数量是试销时的两倍”即可列方程求解; (2)先分别求得两次进的苹果的质量,再分别求得两次销售的利润,从而可以求得结果. (1)设试销时苹果的进货价是x元/斤,由题意得 ...查看答案和解析>>
科目:初中数学 来源:河南省周口市西华县2017-2018学年八年级上学期期末考试数学试卷 题型:单选题
计算正确的是( )
A.  B.
B. 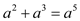 C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源:江苏省扬州市2018届九年级上学期期末考试数学试卷 题型:解答题
如图,△ABC是边长为12的等边三角形,D是BC的中点,E是直线AD上的一个动点,连接EC,将线段EC绕点C逆时针旋转60°得到FC,连接DF.则在点E的运动过程中,DF的最小值是______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com