
如图,在直角坐标平面内,直线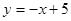 与
与 轴和
轴和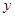 轴分别交于A、B两点,二次函数
轴分别交于A、B两点,二次函数 的图象经过点A、B,且顶点为C.
的图象经过点A、B,且顶点为C.
(1)求这个二次函数的解析式;
(2)求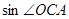 的值;
的值;
(3)若P是这个二次函数图象上位于 轴下方的一点,且
轴下方的一点,且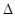 ABP的面积为10,求点P的坐标.
ABP的面积为10,求点P的坐标.
(1)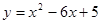
(2)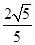
(3)P(4,-3)
解析试题分析:(1)根据直线方程求得点A、B的坐标;然后把点A、B的坐标代入二次函数解析式,通过方程组来求系数b、c的值;
(2)如图,过点C作CH⊥x轴交x轴于点H,构建等腰△AOC.则∠OAC=∠OCA,故sin∠OCA=sin∠OAC=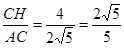 .
.
(3)如图,过P点作PQ⊥x轴并延长交直线y=-x+5于Q.设点P(m,m2-6m+5),Q(m,-m+5),则PQ=-m+5-(m2-6m+5)=-m2+5m.由S△ABP=S△PQB+S△PQA得到:10= (?m2+5m)×5,则易求m的值.注意点P位于第四象限.
(?m2+5m)×5,则易求m的值.注意点P位于第四象限.
试题解析: 解:(1)由直线
解:(1)由直线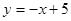 得点B(0,5),A(5,0),
得点B(0,5),A(5,0),
将A、B两点的坐标代入 ,得
,得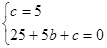 ,解得
,解得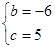
∴抛物线的解析式为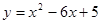
(2)过点C作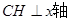 交x轴于点H
交x轴于点H
把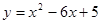 配方得
配方得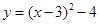 ∴点C(3,-4),
∴点C(3,-4),
∴CH=4,AH=2,AC=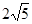 ∴OC=5,
∴OC=5,
∵OA=5∴OA=OC∴
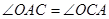
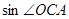 =
=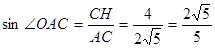

(3)过P点作PQ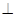 x轴并延长交直线
x轴并延长交直线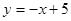 于Q
于Q
设点P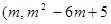 ),Q(m,-m+5)
),Q(m,-m+5)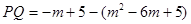 =
=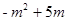
∵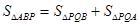
∴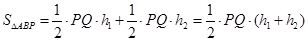
∴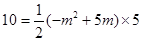
∴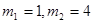
∴P(1,0)(舍去),P(4,-3)
考点:二次函数综合题.


科目:初中数学 来源: 题型:解答题
如图,在Rt△ABC中,∠ACB=90°,AC=8cm,AB=10cm.点P从点A出发,以5cm/s的速度从点A运动到终点B;同时,点Q从点C出发,以3cm/s的速度从点C运动到终点B,连结PQ;过点P作PD⊥AC交AC于点D,将△APD沿PD翻折得到△A′PD,以A′P和PB为邻边作?A′PBE,A′E交射线BC于点F,交射线PQ于点G.设?A′PBE与四边形PDCQ重叠部分图形的面积为Scm2,点P的运动时间为ts.
(1)当t为何值时,点A′与点C重合;
(2)用含t的代数式表示QF的长;
(3)求S与t的函数关系式;
(4)请直接写出当射线PQ将?A′PBE分成的两部分图形的面积之比是1:3时t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
“丹棱冻粑”是眉山著名特色小吃,产品畅销省内外,现有一个产品销售点在经销时发现:如果每箱产品盈利10元,每天可售出50箱;若每箱产品涨价1元,日销售量将减少2箱.
(1)现该销售点每天盈利600元,同时又要顾客得到实惠,那么每箱产品应涨价多少元?
(2)若该销售点单纯从经济角度考虑,每箱产品应涨价多少元才能获利最高?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图1,在平面直角坐标系xOy中,点M为抛物线 的顶点,过点(0,4)作x轴的平行线,交抛物线于点P、Q(点P在Q的左侧),PQ=4.
的顶点,过点(0,4)作x轴的平行线,交抛物线于点P、Q(点P在Q的左侧),PQ=4.
(1)求抛物线的函数关系式,并写出点P的坐标;
(2)小丽发现:将抛物线 绕着点P旋转180°,所得新抛物线的顶点恰为坐标原点O,你认为正确吗?请说明理由;
绕着点P旋转180°,所得新抛物线的顶点恰为坐标原点O,你认为正确吗?请说明理由;
(3)如图2,已知点A(1,0),以PA为边作矩形PABC(点P、A、B、C按顺时针的方向排列), .
.
①写出C点的坐标:C( , )(坐标用含有t的代数式表示);
②若点C在题(2)中旋转后的新抛物线上,求t的值.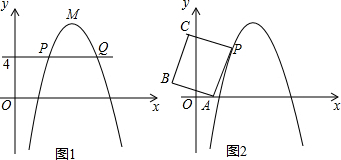
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
一次函数y=x–3的图象与 轴,
轴,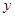 轴分别交于点
轴分别交于点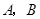 .一个二次函数y=x2+bx+c的图象经过点
.一个二次函数y=x2+bx+c的图象经过点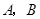 .
.
(1)求点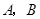 的坐标,并画出一次函数y=x–3的图象;
的坐标,并画出一次函数y=x–3的图象;
(2)求二次函数的解析式并求其图像顶点C的坐标.
(3)求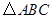 的面积。
的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
今年5月1日起实施《青海省保障性住房准入分配退出和运营管理实施细则》规定:公共租赁住房和廉租住房并轨运行(以下简称并轨房),计划10年内解决低收入人群住房问题.已知第x年(x为正整数)投入使用的并轨房面积为y百万平方米,且y与x的函数关系式为y=-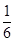 x+5.由于物价上涨等因素的影响,每年单位面积租金也随之上调.假设每年的并轨房全部出租完,预计第x年投入使用的并轨房的单位面积租金z与时间x满足一次函数关系如下表:
x+5.由于物价上涨等因素的影响,每年单位面积租金也随之上调.假设每年的并轨房全部出租完,预计第x年投入使用的并轨房的单位面积租金z与时间x满足一次函数关系如下表:
| 时间x(单位:年,x为正整数) | 1 | 2 | 3 | 4 | 5 | … |
| 单位面积租金z(单位:元/平方米) | 50 | 52 | 54 | 56 | 58 | |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,直线y=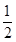 x+m与抛物线y=
x+m与抛物线y=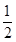 x2-2x+l交于不同的两点M、N(点M在点N的左侧).
x2-2x+l交于不同的两点M、N(点M在点N的左侧).
(1)设抛物线的顶点为B,对称轴l与直线y=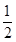 x+m的交点为C,连结BM、BN,若S△MBC=
x+m的交点为C,连结BM、BN,若S△MBC=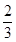 S△NBC,求直线MN的解析式;
S△NBC,求直线MN的解析式;
(2)在(1)条件下,已知点P(t,0)为x轴上的一个动点,
①若△PMN为直角三角形,求点P的坐标.
②若∠MPN>90°,则t的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:计算题
如图所示,已知平面直角坐标系xOy,抛物线过点A(4,0)、B(1,3)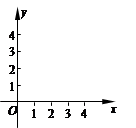
【小题1】求该抛物线的表达式,并写出该抛物线的对称轴和顶点坐标;
【小题2】记该抛物线的对称轴为直线l,设抛物线上的点P(m,n)在第四象限,点P关于直线l的对称点为E,点E关于y轴的对称点为F,若四边形OAPF的面积为20,求m、n的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com