
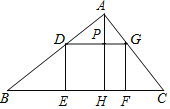
【题目】如图,矩形DEFG的边EF在△ABC的边BC上,顶点D,G分别在边AB,AC上,AH⊥BC,垂足为H,AH交DG于点P,已知BC=6,AH=4.当矩形DEFG面积最大时,HP的长是( )
A.1B.2C.3D.4
科目:初中数学 来源: 题型:
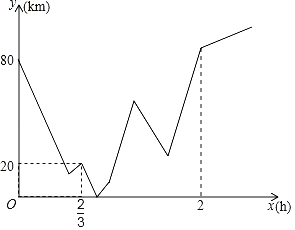
【题目】A、B两地之间有一修理厂C,一日小海和王陆分别从A、B两地同时出发相向而行,王陆开车,小海骑摩托.二人相遇时小海的摩托车突然出故障无法前行,王陆决定将小海和摩托车一起送回到修理厂C后再继续按原路前行,王陆到达A地后立即返回B地,到B地后不再继续前行,等待小海前来(装载摩托车时间和掉头时间忽略不计),整个行驶过程中王陆速度不变,而小海在修理厂花了十分钟修好摩托车,为了赶时间,提速![]() 前往目的地B,小海到达B地后也结束行程,若图象表示的是小海与王陆二人到修理厂C的距离和y(km)与小海出行时间之间x(h)的关系,则当王陆第二次与小海在行驶中相遇时,小海离目的地B还有_____km.
前往目的地B,小海到达B地后也结束行程,若图象表示的是小海与王陆二人到修理厂C的距离和y(km)与小海出行时间之间x(h)的关系,则当王陆第二次与小海在行驶中相遇时,小海离目的地B还有_____km.
查看答案和解析>>
科目:初中数学 来源: 题型:
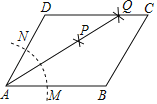
【题目】如图,在平行四边形ABCD中,按以下步骤作图:①以A为圆心,任意长为半径作弧,分别交AB,AD于点M,N;②分别以M,N为圆心,以大于![]() MN的长为半径作弧,两弧相交于点P;③作AP射线,交边CD于点Q,若DQ=2QC,BC=3,则平行四边形ABCD周长为________.
MN的长为半径作弧,两弧相交于点P;③作AP射线,交边CD于点Q,若DQ=2QC,BC=3,则平行四边形ABCD周长为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
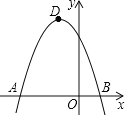
【题目】在平面直角坐标系中,二次函数y=-x2-bx+c的图象经过点A,点B(1,0)和点C(0,3).点D是抛物线的顶点.
(1)求二次函数的解析式和点D的坐标
(2)直线y=kx+n(k≠0)与抛物线交于点M,N,当△CMN的面积被y轴平分时,求k和n应满足的条件
(3)抛物线的对称轴与x轴交于点E,将抛物线向下平移m(m>0)个单位,平移后抛物线与y轴交于点C′,连接DC′,OD,是否存在OD平分∠C′DE的情况?若存在,求出m的值;若不荐在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是射线
是射线![]() 上一动点,过点
上一动点,过点![]() 作
作![]() ,垂足为点
,垂足为点![]() ,交直线
,交直线![]() 于点
于点![]() .
.
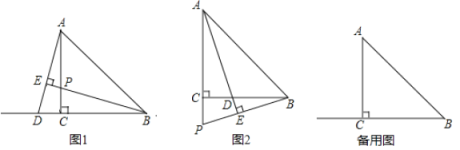
(问题发现)(1)如图1,若点![]() 在
在![]() 的延长线上,试猜想
的延长线上,试猜想![]() ,
,![]() ,
,![]() 之间的数量关系为_______;
之间的数量关系为_______;
(类比探究)(2)如图2,若点![]() 在线段
在线段![]() 上,试猜想
上,试猜想![]() ,
,![]() ,
,![]() 之间的数量关系,并说明理由;
之间的数量关系,并说明理由;
(拓展应用)(3)当点![]() 为
为![]() 的中点时,直接写出线段
的中点时,直接写出线段![]() 的长度.
的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】公司以10元/千克的价格收购一批产品进行销售,经过市场调查获悉,日销售量y(千克)是销售价格x(元/千克)的一次函数,部分数据如表:
销售价格x(元/千克) | 10 | 15 | 20 | 25 | 30 |
日销售量y(千克) | 300 | 225 | 150 | 75 | 0 |
(1)直接写出y与x之间的函数表达式;
(2)求日销售利润为150元时的销售价格;
(3)若公司每销售1千克产品需另行支出a元(0<a<10)的费用,当20≤x≤25时,公司的日获利润的最大值为1215元,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
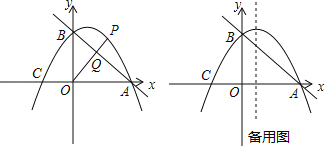
【题目】如图,直线y=﹣![]() x+3与x轴交于点A,与y轴交于点B.抛物线y=﹣
x+3与x轴交于点A,与y轴交于点B.抛物线y=﹣![]() x2+bx+c经过A、B两点,与x轴的另一个交点为C.
x2+bx+c经过A、B两点,与x轴的另一个交点为C.
(1)求抛物线的解析式;
(2)点P是第一象限抛物线上的点,连接OP交直线AB于点Q.设点P的横坐标为m,PQ与OQ的比值为y,求y与m的关系式,并求出PQ与OQ的比值的最大值;
(3)点D是抛物线对称轴上的一动点,连接OD、CD,设△ODC外接圆的圆心为M,当sin∠ODC的值最大时,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A的坐标为![]() 轴于点
轴于点![]() ,反比例函数
,反比例函数![]() 的图像的一支分别交
的图像的一支分别交![]() 于点
于点![]() ,延长
,延长![]() 交反比例函数的图像的另一支于点E,已知D的纵坐标为
交反比例函数的图像的另一支于点E,已知D的纵坐标为![]() .
.
(1)求反比例函数的解析式及直线OA的解析式;
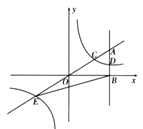
(2)连接BC,已知![]() ,求
,求![]()
(3)若在![]() 轴上有两点
轴上有两点![]() ,将直线
,将直线![]() 绕点
绕点![]() 旋转,仍与
旋转,仍与![]() 交于
交于![]() ,能否构成以
,能否构成以![]() 为顶点的四边形为菱形,如果能请求出
为顶点的四边形为菱形,如果能请求出![]() 的值,如果不能说明理由.
的值,如果不能说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E是平行四边形ABCD的边CD的中点,延长AE交BC的延长线于点F.
(1)求证:△ADE≌△FCE.
(2)若∠BAF=90°,BC=5,EF=3,求平行四边形ABCD的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com