[题目]如图.顺次连接边长为1的正方形ABCD四边的中点.得到四边形A1B1C1D1 . 然后顺次连接四边形A1B1C1D1四边的中点.得到四边形A2B2C2D2 . 再顺次连接四边形A2B2C2D2四边的中点.得到四边形A3B3C3D3 . -.按此方法得到的四边形A8B8C8D8的周长为．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】如图，顺次连接边长为1的正方形ABCD四边的中点，得到四边形A1B1C1D1 ，然后顺次连接四边形A1B1C1D1四边的中点，得到四边形A2B2C2D2 ，再顺次连接四边形A2B2C2D2四边的中点，得到四边形A3B3C3D3 ， …，按此方法得到的四边形A8B8C8D8的周长为．

【答案】
【解析】解：顺次连接正方形ABCD四边的中点得正方形A1B1C1D1 ，则得正方形A1B1C1D1的面积为正方形ABCD面积的一半，即，则周长是正方形ABCD的；顺次连接正方形A1B1C1D1中点得正方形A2B2C2D2 ，则正方形A2B2C2D2的面积为正方形A1B1C1D1面积的一半，即正方形ABCD的，则周长是正方形ABCD的；
顺次连接正方形A2B2C2D2得正方形A3B3C3D3 ，则正方形A3B3C3D3的面积为正方形A2B2C2D2面积的一半，即正方形ABCD的，则周长是正方形ABCD的；
顺次连接正方形A3B3C3D3中点得正方形A4B4C4D4 ，则正方形A4B4C4D4的面积为正方形A3B3C3D3面积的一半，即正方形ABCD的，则周长是正方形ABCD的；
…
故第n个正方形周长是原来的，
以此类推：正方形A8B8C8D8周长是原来的，
∵正方形ABCD的边长为1，周长为4，
∴按此方法得到的四边形A8B8C8D8的周长为，
所以答案是：．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】解方程
（1）x2﹣4x+1=0
（2）3（x﹣2）2=x（x﹣2）．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】【问题提出】学习了三角形全等的判定方法（即“SAS”、“ASA”、“AAS”、“SSS”）和直角三角形全等的判定方法（即“HL”）后，我们继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究．
【初步思考】
我们不妨将问题用符号语言表示为：在△ABC和△DEF中，AC=DF，BC=EF，∠B=∠E，然后，对∠B进行分类，可分为“∠B是直角、钝角、锐角”三种情况进行探究．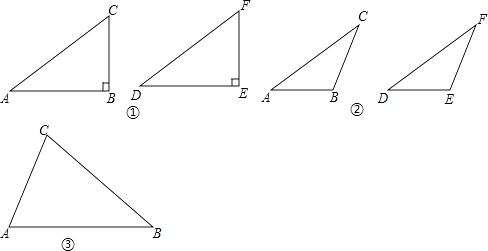

【深入探究】
第一种情况：当∠B是直角时，△ABC≌△DEF．
（1）如图①，在△ABC和△DEF，AC=DF，BC=EF，∠B=∠E=90°，根据，可以知道Rt△ABC≌Rt△DEF．第二种情况：当∠B是钝角时，△ABC≌△DEF．
（2）如图②，在△ABC和△DEF，AC=DF，BC=EF，∠B=∠E，且∠B、∠E都是钝角，求证：△ABC≌△DEF．第三种情况：当∠B是锐角时，△ABC和△DEF不一定全等．
（3）在△ABC和△DEF，AC=DF，BC=EF，∠B=∠E，且∠B、∠E都是锐角，请你用尺规在图③中作出△DEF，使△DEF和△ABC不全等．（不写作法，保留作图痕迹）
（4）∠B还要满足什么条件，就可以使△ABC≌△DEF？请直接写出结论：在△ABC和△DEF中，AC=DF，BC=EF，∠B=∠E，且∠B、∠E都是锐角，若，则△ABC≌△DEF．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】我市启动了第二届“美丽港城，美在阅读”全民阅读活动，为了解市民每天的阅读时间情况，随机抽取了部分市民进行调查，根据调查结果绘制如下尚不完整的频数分布表：

阅读时间 x（min）	0≤x＜30	30≤x＜60	60≤x＜90	x≥90	合计
频数	450	400		50
频率		0.4	0.1		1

（1）补全表格；
（2）将每天阅读时间不低于60min的市民称为“阅读爱好者”，若我市约有500万人，请估计我市能称为“阅读爱好者”的市民约有多少万人？

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】已知，如图，四边形ABCD中，AB=3cm，AD=4cm，BC=13cm，CD=12cm，且∠A=90°，求四边形ABCD的面积.

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】某公司为了解员工对“六五”普法知识的知晓情况，从本公司随机选取40名员工进行普法知识考查，对考查成绩进行统计（成绩均为整数，满分100分），并依据统计数据绘制了如下尚不完整的统计表．解答下列问题：

组别	分数段/分	频数/人数	频率
1	50.5～60.5	2	a
2	60.5～70.5	6	0.15
3	70.5～80.5	b	c
4	80.5～90.5	12	0.30
5	90.5～100.5	6	0.15
合计		40	1.00

（1）表中a= ， b= ， c=；
（2）请补全频数分布直方图；
（3）该公司共有员工3000人，若考查成绩80分以上（不含80分）为优秀，试估计该公司员工“六五”普法知识知晓程度达到优秀的人数．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】已知：如图，在平面直角坐标系中，O为坐标原点，四边形OABC是矩形，点A、C的坐标分别为A（7，0），C（0，4），点D的坐标为（5，0），点P在BC边上运动. 当△ODP是腰长为5的等腰三角形时，点P的坐标为______________.

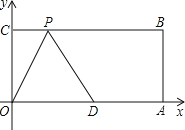
查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】我们用[a]表示不大于a的最大整数，例如：[2.5]=2，[3]=3，[﹣2.5]=﹣3；用＜a＞表示大于a的最小整数，例如：＜2.5＞=3，＜4＞=5，＜﹣1.5＞=﹣1．解决下列问题：
（1）[﹣4.5]= ，＜3.5＞= ．
（2）若[x]=2，则x的取值范围是；若＜y＞=﹣1，则y的取值范围是．
（3）已知x，y满足方程组，求x，y的取值范围．