
【题目】将背面相同,正面分别标有数字1、2、3、4的四张卡片洗匀后,背面朝上放在桌面上,先从中随机的抽取一张卡片(不放回),将该卡片正面上的数字作为十位数字,再随机的抽取一张卡片,将该卡片正面上的数字作为个位数字,则组成的两位数恰好是4的倍数的概率是多少?请用树状图或列表法加以说明.
科目:初中数学 来源: 题型:
【题目】已知:![]() ,OE平分
,OE平分![]() ,点A、B、C分别是射线OM、OE、ON上的动点
,点A、B、C分别是射线OM、OE、ON上的动点![]() 、B、C不与点O重合
、B、C不与点O重合![]() ,连接AC交射线OE于点
,连接AC交射线OE于点![]() 设
设![]() .
.

![]() 如图1,若
如图1,若![]() ,则
,则
![]() 的度数是______;
的度数是______;
![]() 当
当![]() 时,
时,![]() ______;当
______;当![]() 时,
时,![]() ______.
______.
![]() 如图2,若
如图2,若![]() ,则是否存在这样的x的值,使得
,则是否存在这样的x的值,使得![]() 中有两个相等的角?若存在,求出x的值;若不存在,说明理由.
中有两个相等的角?若存在,求出x的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() 于点F,
于点F,![]() 于点M,
于点M,![]() ,
,![]() ,已知动点E以
,已知动点E以![]() 的速度从A点向F点运动,同时动点G以
的速度从A点向F点运动,同时动点G以![]() 的速度从C点向A点运动,当其中一点到达终点时,另一点随之停止运动,设运动时间为t.
的速度从C点向A点运动,当其中一点到达终点时,另一点随之停止运动,设运动时间为t.

![]() ______;
______;
![]() 求
求![]() 的值;
的值;
![]() 在整个运动过程中,当t取何值时,
在整个运动过程中,当t取何值时,![]() 与
与![]() 全等.
全等.
查看答案和解析>>
科目:初中数学 来源: 题型:
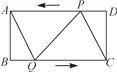
【题目】如图,在矩形ABCD中,AB=4 cm,BC=8 cm,点P从点D出发向点A运动,运动到点A即停止;同时点Q从点B出发向点C运动,运动到点C即停止.点P,Q的速度的速度都是1 cm/s,连结PQ,AQ,CP,设点P,Q运动的时间为t(s).
(1)当t为何值时,四边形ABQP是矩形?
(2)当t为何值时,四边形AQCP是菱形?
(3)分别求出(2)中菱形AQCP的周长和面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,∠A=60°,点E,F分别在AB,AC上,把∠A沿着EF对折,使点A落在BC上点D处,且使ED⊥BC. 
(1)猜测AE与BE的数量关系,并说明理由;
(2)求证:四边形AEDF是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】邻边不相等的平行四边形纸片,剪去一个菱形,余下一个四边形,称为第一次操作;在余下的四边形纸片中再剪去一个菱形,又余下一个四边形,称为第二 次操作;……依此类推,若第n次操作余下的四边形是菱形,则称原平行四边形为n阶准菱形.如图1,平行四边形ABCD中,若AB=1,BC=2,则平行四 边形ABCD为1阶准菱形.

(I)判断与推理:
(i)邻边长分别为2和3的平行四边形是_________阶准菱形;
(ii)为了剪去一个菱形,进行如下操作:如图2,把平行四边形ABCD沿BE折叠(点E在AD上),使点A落在BC边上的点F,得到四边形ABFE,请证明四边形ABFE是菱形.

(Ⅱ)操作与计算:
已知平行四边形ABCD的邻边长分别为l,a(a>1),且是3阶准菱形,请画出平行四边形ABCD及裁剪线的示意图,并在图形下方写出a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中AB∥CD,对角线AC,BD相交于O,点E,F分别为BD上两点,且BE=DF,∠AEF=∠CFB.
(1)求证:四边形ABCD是平行四边形;
(2)若AC=2OE,试判断四边形AECF的形状,并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com