
【题目】如图,在Rt△ABC中,∠ACB=90°,∠BAC=60°.把△ABC绕点A按顺时针方向旋转60°后得到△AB′C′,若AB=8,则线段BC在上述旋转过程中所扫过部分(阴影部分)的面积是( )
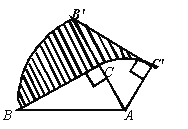
A. 8π B. 6π C. 4π D. 2π
【答案】A
【解析】分析: 根据阴影部分的面积是:扇形BAB′的面积+S△AB′C′-S△ABC-扇形CAC′的面积,分别求得:扇形BAB′的面积S△AB′C′,S△ABC以及扇形CAC′的面积,即可求解.
详解: 扇形BAB′的面积是: ![]() =
= ![]() ,
,
在直角△ABC中,BC=ABsin60°=8×![]() =4
=4![]() ,AC=
,AC=![]() AB=4,
AB=4,
S△ABC=S△AB′C′=![]() ACBC=
ACBC=![]() ×4
×4![]() ×4=16
×4=16![]() .
.
扇形CAC′的面积是:![]() =
=![]() ,
,
则阴影部分的面积是:扇形BAB′的面积+S△AB′C′-S△ABC-扇形CAC′的面积
=![]() -
- ![]() =8π.
=8π.
故选:A.
点睛: 本题考查了扇形的面积的计算,正确理解阴影部分的面积是:扇形BAB′的面积+S△AB′C′-S△ABC-扇形CAC′的面积是关键.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源: 题型:
【题目】为了解高中学生每月用掉中性笔笔芯的情况,随机抽查了30名高中学生进行调查,并将调查的数据制成如下的表格:
月平均用中性笔笔芯(根) | 4 | 5 | 6 | 7 | 8 | 9 |
被调查的学生数 | 7 | 4 | 9 | 5 | 2 | 3 |
请根据以上信息,解答下列问题:
(1)被调查的学生月平均用中性笔笔芯数大约________根;
(2)被调查的学生月用中性笔笔芯数的中位数为________根,众数为________根;
(3)根据样本数据,若被调查的高中共有1000名学生,试估计该校月平均用中性笔笔芯数9根的约多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】西瓜经营户以2元/千克的价格购进一批小型西瓜,以3元/千克的价格出售,每天可售出200千克,为了促销,该经营户决定降价销售,经调查发现,这种小型西瓜每降价0.1元/千克,每天可多售出40千克,另外,每天的房租等固定成本共24元,设每千克降价x元每天销量为y千克.
(1)求y与x的函数关系式;
(2)如何定价,才能使每天获得的利润为200元,且使每天的销量较大?
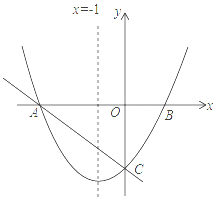
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知
与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知![]() ,
,![]() .
.
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 在抛物线的对称轴上是否存在点P,使
在抛物线的对称轴上是否存在点P,使![]() 是以CD为腰的等腰三角形?如果存在,直接写出P点的坐标;如果不存在,请说明理由;
是以CD为腰的等腰三角形?如果存在,直接写出P点的坐标;如果不存在,请说明理由;
![]() 点E时线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,
点E时线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,![]() 的面积最大?求出
的面积最大?求出![]() 的最大面积及此时E点的坐标.
的最大面积及此时E点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李老师准备购买若干个某种笔记本奖励学生,甲、乙两家商店都有足够数量的这种笔记本,其标价都是每个6元,甲商店的促销方案是:购买这种笔记本数量不超过5个时,原价销售;超过5个时,超过部分按原价的7折销售.乙商店的销售方案是:一律按标价的8折销售.
(1)若李老师要购买![]() 个这种笔记本,请用含
个这种笔记本,请用含![]() 的式子分别表示李老师到甲商店和乙商店购买全部这种笔记本所需的费用.
的式子分别表示李老师到甲商店和乙商店购买全部这种笔记本所需的费用.
(2)李老师购买多少个这种笔记本时,到甲、乙两家商店购买所需费用相同?
(3)若李老师需要20个这种笔记本,则到甲、乙哪家商店购买更优惠?
查看答案和解析>>
科目:初中数学 来源: 题型:
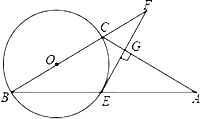
【题目】如图,已知△ABC中,AC=BC,以BC为直径的⊙O交AB于E,过点E作EG⊥AC于G,交BC的延长线于F.
(1)求证:FE是⊙O的切线;
(2)若FE=4,FC=2,求⊙O的半径及CG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD是边BC上的中线,过点A作AE∥BC,过点D作DE∥AB,DE与AC、AE分别交于点O、点E,连接EC.
(1)求证:AD=EC;
(2)当∠BAC=Rt∠时,求证:四边形ADCE是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知线段![]()
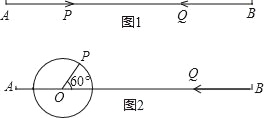
(1)如图1,点![]() 沿线段
沿线段![]() 自点
自点![]() 向点
向点![]() 以
以![]() 的速度运动,同时点
的速度运动,同时点![]() 沿线段点
沿线段点![]() 向点
向点![]() 以
以![]() 的速度运动,几秒钟后,
的速度运动,几秒钟后,![]() 两点相遇?
两点相遇?
(2)如图1,几秒后,点![]() 两点相距
两点相距![]() ?
?
(3)如图2,![]() ,
,![]() ,当点
,当点![]() 在
在![]() 的上方,且
的上方,且![]() 时,点
时,点![]() 绕着点
绕着点![]() 以30度/秒的速度在圆周上逆时针旋转一周停止,同时点
以30度/秒的速度在圆周上逆时针旋转一周停止,同时点![]() 沿直线
沿直线![]() 自
自![]() 点向
点向![]() 点运动,假若点
点运动,假若点![]() 两点能相遇,求点
两点能相遇,求点![]() 的运动速度.
的运动速度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com