
【题目】如图,P是正三角形ABC内的一点,且PA=5,PB=12,PC=13,若将△PAC绕点A逆时针旋转后,得到△P′AB,求点P与点P′之间的距离及∠APB的度数.

【答案】点P与点P′之间的距离为5,∠APB的度数为150°.
【解析】
试题分析:先根据等边三角形的性质得AB=AC,∠BAC=60°,再利用旋转的性质得∠P′AP=∠BAC=60°,AP′=AP,BP′=CP=13,于是可判断△AP′P为等边三角形,得到PP′=AP=5,∠APP′=60°,接着根据勾股定理的逆定理证明△BPP′为直角三角形,且∠BPP′=90°,然后利用∠APB=∠APP′+∠BPP′求出∠APB的度数.
试题解析:∵△ABC为等边三角形,∴AB=AC,∠BAC=60°,
∵△PAC绕点A逆时针旋转后,得到△P′AB,
∴∠P′AP=∠BAC=60°,AP′=AP,BP′=CP=13,
∴△AP′P为等边三角形,
∴PP′=AP=5,∠APP′=60°,
在△BPP′中,∵PP′=5,BP=12,BP′=13,
∴PP′2+BP2=BP′2,
∴△BPP′为直角三角形,∠BPP′=90°,
∴∠APB=∠APP′+∠BPP′=60°+90°=150°.
答:点P与点P′之间的距离为5,∠APB的度数为150°.



 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:初中数学 来源: 题型:
【题目】在一个不透明的布袋里装有4个标号为1、2、-3、-4.的小球,它们的材质、形状、大小完全相同,小凯从布袋里随机取出一个小球,记下数字为x,小敏从剩下的3个小球中随机取出一个小球,记下数字为y,这样确定了点P的坐标(x,y).
(1)小凯从布袋里随机取出一个小球,记下数字为x,求x为负数的概率;
(2)请你运用画树状图或列表的方法,写出点P所有可能的坐标;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】方程-x2+3x=1用公式法求解,先确定a , b , c的值,正确的是( )
A.a=-1,b=3,c=-1
B.a=-1,b=3,c=1
C.a=-1,b=-3,c=-1
D.a=1,b=-3,c=-1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电视台“走基层”栏目的一位记者赴360km外的农村采访,全程的前一部分为高速公路,后一部分为乡村公路.如果汽车在高速公路和乡村公路上分别以某一速度匀速行驶,汽车行驶的路程y(单位:km)与时间x(单位:h)之间的关系如图所示,那么汽车在乡村公路上的行驶速度为km/h. 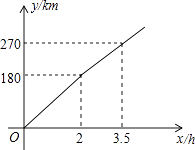
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把几个图形拼成一个新的图形,再通过两种不同的方法计算同一个图形的面积,可以得到一个等式,也可以求出一些不规则图形的面积. 例如,由1,可得等式:(a+2b)(a+b)=a2+3ab+2b2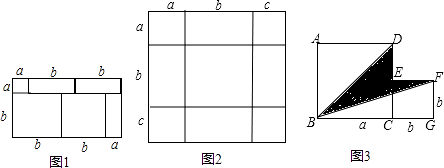
(1)如图2,将几个面积不等的小正方形与小长方形拼成一个边长为a+b+c的正方形,试用不同的形式表示这个大正方形的面积,你能发现什么结论?请用等式表示出来.
(2)利用(1)中所得到的结论,解决下面的问题:已知a+b+c=11,ab+bc+ac=38,求a2+b2+c2的值.
(3)如图3,将两个边长分别为a和b的正方形拼在一起,B,C,G三点在同一直线上,连接BD和BF.若这两个正方形的边长满足a+b=10,ab=20,请求出阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据报道,2017年11月11日淘宝网一天的销售额为1682亿元,这个数据用科学记数法表示为( )
A. 1682×108 B. 16.82×1010 C. 1.682×1010 D. 1.682×1011
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图△ADF和△BCE中,∠A=∠B,点D、E、F、C在同﹣直线上,有如下三个关系式:①AD=BC;②DE=CF;③BE∥AF。

(1)请用其中两个关系式作为条件,另一个作为结论,写出所有你认为正确的命题.(用序号写出命题书写形式,如:如果①、②,那么③)
(2)选择(1)中你写出的一个命题,说明它正确的理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com