
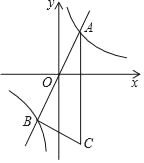
【题目】如图,反比例函数的图象与正比例函数y=2x的图象相交于A(1,a),B两点,点C在第四象限,CA∥y轴,∠ABC=90°
(1)求反比例函数的解析式及点B的坐标;
(2)求tanC的值.
【答案】(1)反比例函数解析式为y=![]() ;点B的坐标为(﹣1,﹣2);(2)2.
;点B的坐标为(﹣1,﹣2);(2)2.
【解析】
(1)先利用正比例函数解析式确定A(1,2),再根据A点坐标即可得到反比例函数解析式,然后依据点A和点B关于原点对称得到B点坐标;
(2)依据∠ABC=∠ADO=90°,可得∠C=∠AOD,再根据A(1,2),即可得出tanC=tan∠AOD=![]() =2.
=2.
解:(1)把A(1,a)代入y=2x,得a=2,
∴A(1,2),
把A(1,2)代入y=![]() ,得k=1×2=2,
,得k=1×2=2,
∴反比例函数解析式为y=![]() ,
,
∵点A和点B关于原点对称,
∴点B的坐标为(﹣1,﹣2);
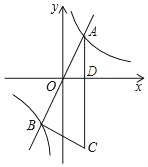
(2)如图,∵CA∥y轴,∠ABC=90°,
∴∠ABC=∠ADO=90°,
∴∠C=∠AOD,
又∵A(1,2),
∴AD=2,OD=1,
∴tanC=tan∠AOD=![]() =2.
=2.
故答案为:(1)反比例函数解析式为y=![]() ;点B的坐标为(﹣1,﹣2);(2)2.
;点B的坐标为(﹣1,﹣2);(2)2.


科目:初中数学 来源: 题型:
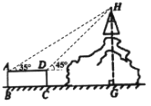
【题目】如图,山上有一座高塔,山脚下有一圆柱形建筑物平台,高塔及山的剖面与圆柱形建筑物平台的剖面ABCD在同一平面上,在点A处测得塔顶H的仰角为35°,在点D处测得塔顶H的仰角为45°,又测得圆柱形建筑物的上底面直径AD为6m,高CD为2.8m,则塔顶端H到地面的高度HG为( )
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() )
)
A.10.8mB.14mC.16.8mD.29.8m
查看答案和解析>>
科目:初中数学 来源: 题型:
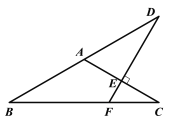
【题目】如图,在△ABC中,AB=AC,∠BAC=120°,线段AC的垂直平分线交BC于点F,交AC于点E,交BA的延长线于点D.若DE=3,则BF=( ).
A.4B.3C.2D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
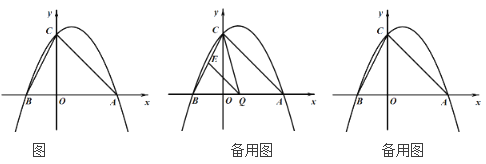
【题目】如图已知抛物线与![]() 轴交于点C(0,4),与
轴交于点C(0,4),与![]() 轴交于A(
轴交于A(![]() ,0)、B(
,0)、B(![]() ,0),其中
,0),其中![]() ,
,![]() 为方程
为方程![]() 的两个根.
的两个根.
(1)求该抛物线的解析式;
(2)点Q是线段AB上的动点,过点Q作QE∥AC,交BC于点E,连结CQ,设Q(![]() ,0),△CQE的面积为
,0),△CQE的面积为![]() ,求
,求![]() 关于
关于![]() 的函数关系式及△CQE的面积的最大值;
的函数关系式及△CQE的面积的最大值;
(3)点M的坐标为(2,0),问:在直线AC上,是否存在点F,使得△OMF是等腰三角形?若存在,请求出点F的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】教材呈现:下图是华师版八年级上册数学教材第94页的部分内容.
线段垂直平分线
我们已知知道线段是轴对称图形,线段的垂直一部分线是线段的对称轴,如图直线![]() 是线段
是线段![]() 的垂直平分线,
的垂直平分线,![]() 是
是![]() 上任一点,连结
上任一点,连结![]() 、
、![]() ,将线段
,将线段![]() 与直线
与直线![]() 对称,我们发现
对称,我们发现![]() 与
与![]() 完全重合,由此都有:线段垂直平分线的性质定理,线段垂直平分线上的点到线段的距离相等.
完全重合,由此都有:线段垂直平分线的性质定理,线段垂直平分线上的点到线段的距离相等.
已知:如图,![]() ,垂足为点
,垂足为点![]() ,
,![]() ,点
,点![]() 是直线
是直线![]() 上的任意一点.
上的任意一点.
求证:![]() .
.
图中的两个直角三角形![]() 和
和![]() ,只要证明这两个三角形全等,便可证明
,只要证明这两个三角形全等,便可证明![]() (请写出完整的证明过程)
(请写出完整的证明过程)
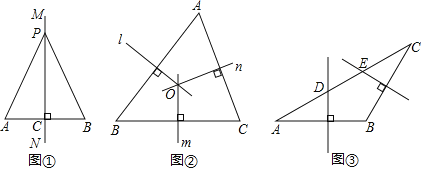
请根据教材中的分析,结合图①,写出“线段垂直平分线的性质定理”完整的证明过程,定理应用.
(1)如图②,在![]() 中,直线
中,直线![]() 、
、![]() 、
、![]() 分别是边
分别是边![]() 、
、![]() 、
、![]() 的垂直平分线.
的垂直平分线.
求证:直线![]() 、
、![]() 、
、![]() 交于点.
交于点.
(2)如图③,在![]() 中,
中,![]() ,边
,边![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,边
,边![]() 的垂直平分线交
的垂直平分线交![]() 于点
于点![]() ,若
,若![]() ,
,![]() ,则
,则![]() 的长为_______.
的长为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织全校学生进行了一次“社会主义核心价值观”知识竞赛,赛后随机抽取了各年级部分学生成绩进行统计,制作如下频数分布表和频数分布直方图.请根据图表中提供的信息,解答下列问题:
分数段( | 频数 | 频率 |
| 4 | 0.1 |
| 8 |
|
|
| 0.3 |
| 10 | 0.25 |
| 6 | 0.15 |
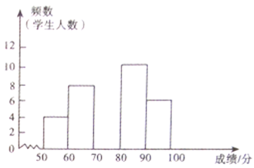
(1)请求出该校随机抽取了____学生成绩进行统计;
(2)表中![]() ____,
____,![]() ____,并补全直方图;
____,并补全直方图;
(3)若用扇形统计图描述此成绩统计分布情况,则分数段![]() 对应扇形的圆心角度数是___
对应扇形的圆心角度数是___![]() ;
;
(4)若该校共有学生8000人,请估计该校分数在![]() 的学生有多少人?
的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
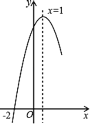
【题目】抛物线![]() 经过点(﹣2,0),且对称轴为直线x=1,其部分图象如图所示.对于此抛物线有如下四个结论:
经过点(﹣2,0),且对称轴为直线x=1,其部分图象如图所示.对于此抛物线有如下四个结论:
①![]() ;
;
②![]() >
>![]() ;
;
③若n>m>0,则![]() 时的函数值小于
时的函数值小于![]() 时的函数值;
时的函数值;
④点(![]() ,0)一定在此抛物线上.
,0)一定在此抛物线上.
其中正确结论的个数是( )
A.4个B.3个
C.2个D.1个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com