
【题目】如图,在△ABC中,∠ACB=90°,点P在∠BCA平分线CD上,且PA=PB.
(1)用尺规作出符合要求的点P(保留作图痕迹,不需要写作法);
(2)判断△ABP的形状(不需要写证明过程)

【答案】(1)见解析;(2)等腰直角三角形.
【解析】
(1)由PA=PB知点P同时还在线段AB的中垂线上,据此作图可得;
(2)点P分别作PE⊥AC、PF⊥CB,垂足为E、F,由全等三角形的判定定理得出Rt△APE≌Rt△BPF,再由全等三角形的性质即可判断出△ABP是等腰直角三角形.
(1)如图所示,点P即为所求;
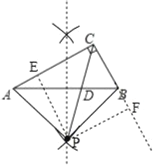
(2)△ABP是等腰直角三角形,
理由如下:过点P分别作PE⊥AC、PF⊥CB,垂足为E、F.
∵PC平分∠ACB,PE⊥AC、PF⊥CB,垂足为E、F,
∴PE=PF.
在Rt△APE与Rt△BPF中,
∵![]() ,
,
∴Rt△APE≌Rt△BPF.
∴∠APE=∠BPF,
∵∠PEC=90°,∠PFC=90°,∠ECF=90°,
∴∠EPF=90°,
∴∠APB=90°.
又∵PA=PB,
∴△ABP是等腰直角三角形.


 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案科目:初中数学 来源: 题型:
【题目】解不等式组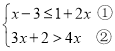 请结合题意填空,完成本题的解答.
请结合题意填空,完成本题的解答.
(Ⅰ)解不等式①,得___________;
(Ⅱ)解不等式②,得___________;
(Ⅲ)把不等式①和②的解集在数轴上表示出来:
![]()
(Ⅳ)原不等式组的解集为___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场进行促销活动,出售一种优惠购物卡(注:此卡只作为购物优惠凭证不能顶替货款),花300元买这种卡后,凭卡可在这家商场按标价的8折购物.若不够卡购物和使用优惠卡购物分别视为方式一购物和方式二购物,且设顾客购买商品的金额为![]() 元.
元.
(Ⅰ)根据题意,填写下表:
商品金额(元) | 300 | 600 | 1000 | … |
|
方式一的总费用(元) | 300 | 600 | 1000 | … | |
方式二的总费用(元) | 540 | … |
(Ⅱ)顾客购买多少元金额的商品时,买卡与不买卡花钱相等?
(Ⅲ)小张要买一台标价为3500元的冰箱,如何购买合算?小张能节省多少元钱?
(Ⅳ)小张按合算的方案,把这台冰箱买下,如果该商场还能盈利![]() ,那么这台冰箱的进价是多少元?
,那么这台冰箱的进价是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
我们知道一次函数![]() (
(![]() ,
,![]() 是常数)的图象是一条直线,到高中学习时,直线通常写成
是常数)的图象是一条直线,到高中学习时,直线通常写成![]() (
(![]() ,
,![]() 是常数)的形式,点
是常数)的形式,点![]() 到直线
到直线![]() 的距离可用公式
的距离可用公式![]() 计算.
计算.
例如:求点![]() 到直线
到直线![]() 的距离.
的距离.
解:∵![]()
∴![]() 其中
其中![]()
∴点![]() 到直线
到直线![]() 的距离为:
的距离为:
![]()
根据以上材料解答下列问题:
(1)求点![]() 到直线
到直线![]() 的距离;
的距离;
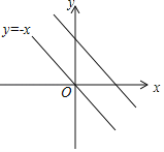
(2)如图,直线![]() 沿
沿![]() 轴向上平移2个单位得到另一条直线,求这两条平行直线之间的距离.
轴向上平移2个单位得到另一条直线,求这两条平行直线之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx﹣5(a≠0)与x轴交于点A(﹣5,0)和点B(3,0),与y轴交于点C.
(1)求该抛物线的解析式;
(2)若点E为x轴下方抛物线上的一动点,当S△ABE=S△ABC时,求点E的坐标;
(3)在(2)的条件下,抛物线上是否存在点P,使∠BAP=∠CAE?若存在,求出点P的横坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某出租公司有若干辆同一型号的货车对外出租,每辆货车的日租金实行淡季、旺季两种价格标准,旺季每辆货车的日租金比淡季上涨![]() .据统计,淡季该公司平均每天有
.据统计,淡季该公司平均每天有![]() 辆货车未出租,日租金总收入为
辆货车未出租,日租金总收入为![]() 元;旺季所有的货车每天能全部租出,日租金总收入为
元;旺季所有的货车每天能全部租出,日租金总收入为![]() 元.
元.
(1)该出租公司这批对外出租的货车共有多少辆?淡季每辆货车的日租金多少元?
(2)经市场调查发现,在旺季如果每辆货车的日租金每上涨![]() 元,每天租出去的货车就会减少
元,每天租出去的货车就会减少![]() 辆,不考虑其它因素,每辆货车的日租金上涨多少元时,该出租公司的日租金总收入最高?
辆,不考虑其它因素,每辆货车的日租金上涨多少元时,该出租公司的日租金总收入最高?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E,F分别为BC,CD的中点,连接AE,BF交于点G,将△BCF沿BF对折,得到△BPF,延长FP交BA延长于点Q,下列结论正确的有( )个.
①AE⊥BF;②QB=QF;③FG=![]() AG;④sin∠BQP=
AG;④sin∠BQP=![]() ;⑤SECPG=3S△BGE
;⑤SECPG=3S△BGE

A. 5B. 4C. 3D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
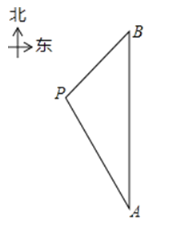
【题目】在一次海上救援中,两艘专业救助船![]() 同时收到某事故渔船的求救讯息,已知此时救助船
同时收到某事故渔船的求救讯息,已知此时救助船![]() 在
在![]() 的正北方向,事故渔船
的正北方向,事故渔船![]() 在救助船
在救助船![]() 的北偏西30°方向上,在救助船
的北偏西30°方向上,在救助船![]() 的西南方向上,且事故渔船
的西南方向上,且事故渔船![]() 与救助船
与救助船![]() 相距120海里.
相距120海里.
(1)求收到求救讯息时事故渔船![]() 与救助船
与救助船![]() 之间的距离;
之间的距离;
(2)若救助船A,![]() 分别以40海里/小时、30海里/小时的速度同时出发,匀速直线前往事故渔船
分别以40海里/小时、30海里/小时的速度同时出发,匀速直线前往事故渔船![]() 处搜救,试通过计算判断哪艘船先到达.
处搜救,试通过计算判断哪艘船先到达.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】当今,越来越多的青少年在观看影片《流浪地球》后,更加喜欢同名科幻小说,该小说销量也急剧上升.书店为满足广大顾客需求,订购该科幻小说若干本,每本进价为20元.根据以往经验:当销售单价是25元时,每天的销售量是250本;销售单价每上涨1元,每天的销售量就减少10本,书店要求每本书的利润不低于10元且不高于18元.
(1)直接写出书店销售该科幻小说时每天的销售量![]() (本)与销售单价
(本)与销售单价![]() (元)之间的函数关系式及自变量的取值范围.
(元)之间的函数关系式及自变量的取值范围.
(2)书店决定每销售1本该科幻小说,就捐赠![]() 元给困难职工,每天扣除捐赠后可获得最大利润为1960元,求
元给困难职工,每天扣除捐赠后可获得最大利润为1960元,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com