
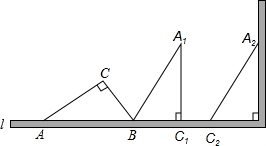
 如图,一个横截面为Rt△ABC的物体,∠ACB=90°,∠CAB=30°,BC=1m,工人师傅要把此物体搬到墙边,先将AB边放在地面(直线l)上,再按顺时针方向绕点B翻转到△A1BC1的位置(BC1在l上),最后沿射线BC1的方向平移到△A2B2C2的位置,其平移的距离为线段AC的长度(此时A2C2恰好靠在墙边).
如图,一个横截面为Rt△ABC的物体,∠ACB=90°,∠CAB=30°,BC=1m,工人师傅要把此物体搬到墙边,先将AB边放在地面(直线l)上,再按顺时针方向绕点B翻转到△A1BC1的位置(BC1在l上),最后沿射线BC1的方向平移到△A2B2C2的位置,其平移的距离为线段AC的长度(此时A2C2恰好靠在墙边).分析 (1)根据直角三角形的三边关系,30°的角所对的直角边是斜边的一半,可以直接确定AB、AC.
(2)根据要求画出路径,再用弧长公式求解路径的长度.
(3)OH扫过的面积=扇形BHH′的面积-扇形BOO′的面积,由此即可计算.
解答 解:(1)∵∠CAB=30°,BC=1米
∴AB=2米,AC=$\sqrt{3}$米.
故答案为2米,$\sqrt{3}$米.
(2)A点经过的路径如图1中所示,
∵∠ABA1=180°-60°=120°,A1A2=AC=$\sqrt{3}$米
∴A点所经过的路径长=$\frac{120}{180}$•π•2+$\sqrt{3}$=$\frac{4}{3}$π+$\sqrt{3}$≈5.9(米).
(3)如图2中,
由题意△BOH≌△BO′H′,
∴OH扫过的面积=扇形BHH′的面积-扇形BOO′的面积=$\frac{120π•H{B}^{2}}{360}$-$\frac{120π•O{B}^{2}}{360}$=$\frac{1}{4}$π.
点评 本题考查旋转变换、平移变换、勾股定理.扇形的面积公式等知识,解题的关键是熟练应用所学知识解决问题,学会把不规则图形转化为规则图形,属于中考常考题型.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 56m | B. | 46m | C. | 36n | D. | 26m |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2015 | B. | -2015 | C. | -$\frac{1}{2015}$ | D. | $\frac{1}{2015}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 10 | B. | 13 | C. | 17 | D. | 18 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com