
| A. | 由a>b得-2a>-2b | B. | 由-1>-2得$\frac{1}{\sqrt{2}}$>$\frac{2}{\sqrt{2}}$ | C. | 由a>b得ac>bc | D. | 由a>b得-a<-b |
分析 根据不等式的性质:不等式的两边都加(或减)同一个数不等号的方向不变,不等式的两边都乘(或除以)同一个正数不等号的方向不变,不等式的两边都乘(或除以)同一个负数不等号的方向改变,可得答案.
解答 解:A、不等式的两边都乘以-2,不等号的方向改变,故A错误;
B、不等式的两边都除以-$\sqrt{2}$,不等号的方向改变,故B错误;
C、c<0,不等号的方向改变,故C错误;
D、不等式的两边都乘以-1,不等号的方向改变,故D正确;
故选:D.
点评 本题考查了不等式的性质,利用不等式的两边都加(或减)同一个数不等号的方向不变,不等式的两边都乘(或除以)同一个正数不等号的方向不变,不等式的两边都乘(或除以)同一个负数不等号的方向改变.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2.79×107 | B. | 2.79×108 | C. | 2.79×109 | D. | 2.79×1010 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
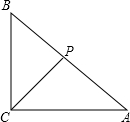 已知:Rt△ABC中,∠ACB=90°,CP平分∠ACB交边AB于点P,点D在边AC上.
已知:Rt△ABC中,∠ACB=90°,CP平分∠ACB交边AB于点P,点D在边AC上.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
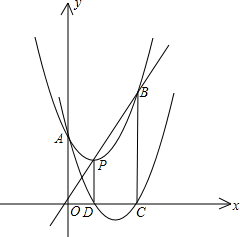 如图,抛物线F:y=ax2+bx+c的顶点为P,抛物线F与y轴交于点A,与直线OP交于点B,过点P作PD⊥x轴于点D,平移抛物线F使其经过点A,D得到抛物线F′:y=a′x2+b′x+c′,抛物线F′与x轴的另一个交点为C,若a,b,c满足b2=2ac,则四边形OABC的形状为( )
如图,抛物线F:y=ax2+bx+c的顶点为P,抛物线F与y轴交于点A,与直线OP交于点B,过点P作PD⊥x轴于点D,平移抛物线F使其经过点A,D得到抛物线F′:y=a′x2+b′x+c′,抛物线F′与x轴的另一个交点为C,若a,b,c满足b2=2ac,则四边形OABC的形状为( )| A. | 平行四边形 | B. | 正方形 | C. | 菱形 | D. | 矩形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
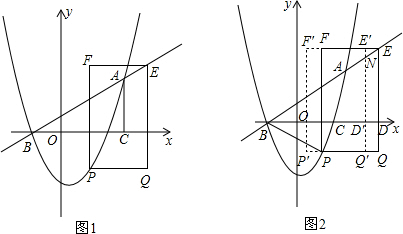
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com