
(10分)在平面直角坐标系中,如图所示,△ABC是边长为2的等边三角形,将△ABC绕着点B按顺时针方向旋转得到△EDB,使得点E落在 轴的正半轴上,连结CE、AD、
轴的正半轴上,连结CE、AD、
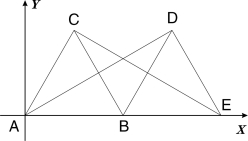
(1)求证:AD=CE;
(2)求AD的长;
(3)求过C、E两点的直线的解析式.
(1)见解析;(2)AD=2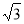 ;(3)
;(3)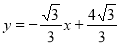
【解析】
试题分析:(1)根据旋转图形可得:AB=BC,BD=BE,∠ABD=∠CBE=120°得出△ABD和△CBE全等,得出所求的结论;(2)作DF⊥AE交x轴于点F,则F为BE的中点,根据Rt△BDF的勾股定理求出DF的长度,根据Rt△ADF的勾股定理求出AD的长度;(3)作CG⊥AB交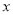 轴于点G,则G为AB的中点,求出AG和CG的长度得出点C的坐标,根据AE=BB+BE求出点E的坐标,然后利用待定系数法求出函数解析式.
轴于点G,则G为AB的中点,求出AG和CG的长度得出点C的坐标,根据AE=BB+BE求出点E的坐标,然后利用待定系数法求出函数解析式.
试题解析:(1)∵△ABC是边长为2的等边三角形,∴AC=AB=BC=2,∠ACB=∠CBA=∠BAC=60°
又△DBE是由△ABC绕着点B按顺时针方向旋转得到的,∴△DBE也是边长为2的等边三角形,
∴∠DBC=180°-60°-60°=60°,AB=BC,BD=BE又∠ABD =∠CBE=120°
∴△ABD≌△CBE(SAS) ∴AD=CE(全等三角形的对应边相等)
(2)作DF⊥AE交x轴于点F,则F为BE的中点,∴BF=1
在Rt△BDF中,BD=2,BF=1,由勾股定理得:DF2=BD2-BF2=4-1=3,∴DF=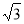
在Rt△ADF中,AF=AB+BF=2+1=3, 由勾股定理得:AD2=AF2+DF2=9+3=12, ∴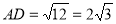
(3)作CG⊥AB交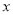 轴于点G,则G为AB的中点,∴AG=1,CG=DF=
轴于点G,则G为AB的中点,∴AG=1,CG=DF=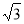
∴C点的坐标是(1, 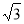 ),又AE=AB+BE=2+2=4, 故E点的坐标是(4,0)
),又AE=AB+BE=2+2=4, 故E点的坐标是(4,0)
设过C、E两点的直线的解析式为y=kx+b,将C,E点的坐标代入解得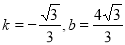 ,
,
∴过C、E两点的直线的解析式为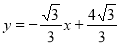
考点:三角形全等的判定与应用、待定系数法求函数解析式.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:2014-2015学年江苏省启东市九年级上学期第二次双周测试数学试卷(解析版) 题型:解答题
如图,⊙O与 的斜边AB相切于点D,与直角边AC相交于E、F两点,连结DE,已知
的斜边AB相切于点D,与直角边AC相交于E、F两点,连结DE,已知 ,⊙O的半径为12,弧DE的长度为
,⊙O的半径为12,弧DE的长度为 .
.

(1)求证:DE∥BC;
(2)若AF=CE,求线段BC的长度.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省东台市九年级上学期第二次月检测数学试卷(解析版) 题型:选择题
如图,在平面直角坐标系中,过格点 ,
, ,
, 作一圆弧,点
作一圆弧,点 与下列格点的连线中,能够与该圆弧相切的是( ).
与下列格点的连线中,能够与该圆弧相切的是( ).

A.点 B.点
B.点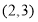 C.点
C.点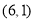 D.点
D.点
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省常熟市九年级上学期期中模拟数学试卷(解析版) 题型:填空题
如果二次函数y=ax2+bx+c的图象的顶点坐标是(2,4),且直线y=x+4依次与y轴和抛物线相交于P、Q、R三点,PQ:QR=1:3,则这个二次函数解析式为 .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省常熟市九年级上学期期中模拟数学试卷(解析版) 题型:选择题
二次函数y=ax2+bx+c的y与x的部分对应值如下表:
x | … | 0 | 1 | 3 | 4 | … |
y | … | 2 | 4 | 2 | ﹣2 | … |
则下列判断中正确的是( )
A.抛物线开口向上
B.抛物线与y轴交于负半轴
C.当x=﹣1时y>0
D.方程ax2+bx+c=0的负根在0与﹣1之间
查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖南省娄底市九年级上学期期末考试数学试卷(解析版) 题型:解答题
(6分) 李大爷的鱼塘今年放养鱼苗10万条,根据这几年的统计分析,鱼苗成活率约为95%,现准备打捞出售,第一网捞出40条,称得平均每条鱼重2.5千克,第二网捞出25条,称得平均每条鱼重2.2千克,第三网捞出35条,称得平均每条鱼重2.8千克,请你帮助李大爷估算今年鱼塘中鱼的总重量.如果每千克售价为4元,那么,李大爷今年的收入如何?
查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖南省娄底市九年级上学期期末考试数学试卷(解析版) 题型:填空题
如图,为估算某河的宽度,在河对岸边选定一个目标点A,在近岸取点B,C,D,使得AB⊥BC,CD⊥BC,点E在BC上,并且点A,E,D在同一条直线上。若测得BE=45m,EC=15m,CD=10m,则河的宽度AB等于 .

查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖北省容城镇三闾学校九年级上学期期中考试数学试卷(解析版) 题型:解答题
某工厂生产的某种产品按质量分为10个档次.第1档次(最低档次)的产品一天能生产76件,每件利润10元.每提高一个档次,每件利润增加2元,但一天产量减少4件.
(1)若生产第x档次的产品一天的总利润为y元(其中x为正整数,且1≤x≤10),求出y关于x的函数关系式;
(2)若生产第x档次的产品一天的总利润为1080元,求该产品的质量档次.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年福建省龙岩市九年级上学期第三次月考数学试卷(解析版) 题型:选择题
二次函数 的最小值是( ).]
的最小值是( ).]
A.-35 B.-30 C.-5 D.20
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com