
【题目】为迎接中国森博会,某商家计划从厂家采购A,B两种产品共20件,产品的采购单价(元/件)是采购数量(件)的一次函数,下表提供了部分采购数据.
采购数量(件) | 1 | 2 | … |
A产品单价(元/件) | 1480 | 1460 | … |
B产品单价(元/件) | 1290 | 1280 | … |
(1)设A产品的采购数量为x(件),采购单价为y1(元/件),求y1与x的关系式;
(2)经商家与厂家协商,采购A产品的数量不少于B产品数量的![]() ,且A产品采购单价不低于1200元,求该商家共有几种进货方案;
,且A产品采购单价不低于1200元,求该商家共有几种进货方案;
(3)该商家分别以1760元/件和1700元/件的销售单价售出A,B两种产品,且全部售完,在(2)的条件下,求采购A种产品多少件时总利润最大,并求最大利润.
【答案】(1)y1=﹣20x+1500(0<x≤20,x为整数);(2)商家共有5种进货方案;(3)当x=15时,W最大=10650.
【解析】试题分析:(1)首先设出函数解析式,然后根据表格将数字代入进行求解;(2)根据题意列出关于x的不等式组,然后根据x为整数,求出x的值;(3)设总利润为w,列出w和x的二次函数关系式,然后根据二次函数的增减性进行求解.
试题解析:(1)设y1与x的关系式y1=kx+b,由表知![]() ,
,
解得k=﹣20,b=1500, 即y1=﹣20x+1500(0<x≤20,x为整数),
(2)根据题意可得 , 解得11≤x≤15, ∵x为整数,
, 解得11≤x≤15, ∵x为整数,
∴x可取的值为:11,12,13,14,15, ∴该商家共有5种进货方案;
(3)令总利润为W,则W=30x2﹣540x+1200=30(x﹣9)2+9570,
∵a=30>0, ∴当x≥9时,W随x的增大而增大, ∵11≤x≤15,
∴当x=15时,W最大=10650;


科目:初中数学 来源: 题型:
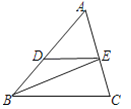
【题目】如图,在△ABC中,BE平分∠ABC交AC于点E,过点E作ED∥BC交AB于点D.
(1)求证:AEBC=BDAC;
(2)如果S△ADE=3,S△BDE=2,DE=6,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数y=![]() 的图象交于点A(﹣3,m+8),B(n,﹣6)两点.
的图象交于点A(﹣3,m+8),B(n,﹣6)两点.
(1)求一次函数与反比例函数的解析式;
(2)求△AOB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数![]() 与一次函数
与一次函数![]() 的图象交于点A(1,8)、B(-4,m).
的图象交于点A(1,8)、B(-4,m).
(1)求k1、k2、b的值;
(2)求△AOB的面积;
(3)请直接写出不等式![]() 的解集;
的解集;
(4)若M(x1,y1)、N(x2,y2)是反比例函数![]() 图象上的两点,且x1<x2,y1<y2,指出点M、N各位于哪个象限,并说明理由.
图象上的两点,且x1<x2,y1<y2,指出点M、N各位于哪个象限,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
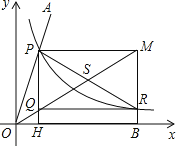
【题目】材料:帕普斯借助函数给出了一种“三等分锐角”的方法,具体如下:
①建立平面直角坐标系,将已知锐角∠AOB的顶点与原点O重合,角的一边OB与x轴正方向重合;
②在平面直角坐标系里,绘制函数y=![]() 的图象,图象与已知角的另一边OA交于点P;
的图象,图象与已知角的另一边OA交于点P;
③以P为圆心,2OP为半径作弧,交函数y=![]() 的图象于点R;
的图象于点R;
④分别过点P和R作x轴和y轴的平行线,两线相交于点M、Q;
⑤连接OM,得到∠MOB,这时∠MOB=![]() ∠AOB.
∠AOB.
根据以上材料解答下列问题:
(1)设点P的坐标为(a,![]() ),点R的坐标为(b,
),点R的坐标为(b,![]() ),则点M的坐标为 ;
),则点M的坐标为 ;
(2)求证:点Q在直线OM上;
(3)求证:∠MOB=![]() ∠AOB;
∠AOB;
(4)应用上述方法得到的结论,如何三等分一个钝角(用文字简要说明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c经过点(![]() 1,0),对称轴为l.则下列结论:①abc>0; ②a-b+c=0; ③2a+c<0; ④a+b<0,其中所有正确的结论是______________
1,0),对称轴为l.则下列结论:①abc>0; ②a-b+c=0; ③2a+c<0; ④a+b<0,其中所有正确的结论是______________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在RtΔABC中,∠C=90°,∠BAC的角平分线AD交BC边于D,以AB上某一点O为圆心作⊙O,使⊙O经过点A和点D,与AB边的另一个交点为E.
(1)判断直线BC与⊙O的位置关系,并说明理由;
(2)若⊙O的半径为4,∠B=30°.求线段BD、BE与劣弧DE所围成的阴影部分的图形面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了编撰祖国的优秀传统文化,某校组织了一次“诗词大会”,小明和小丽同时参加,其中,有一道必答题是:从如图所示的九宫格中选取七个字组成一句唐诗,其答案为“山重水复疑无路”.
(1)小明回答该问题时,对第二个字是选“重”还是选“穷”难以抉择,若随机选择其中一个,则小明回答正确的概率是 ;
(2)小丽回答该问题时,对第二个字是选“重”还是选“穷”、第四个字是选“富”还是选“复”都难以抉择,若分别随机选择,请用列表或画树状图的方法求小丽回答正确的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,三角形A`B`C`是由三角形ABC经过某种平移得到的,点A与点A`,点B与点B`,点C与点C`分别对应,观察点与点坐标之间的关系,解答下列问题:
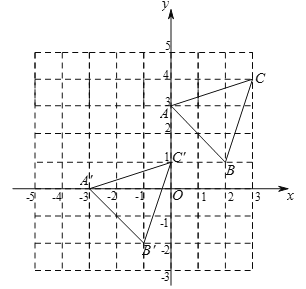
![]() 分别写出点A、点B、点C、点A`、点B`、点C`的坐标,并说明三角形A`B`C`是由三角形ABC经过怎样的平移得到的.
分别写出点A、点B、点C、点A`、点B`、点C`的坐标,并说明三角形A`B`C`是由三角形ABC经过怎样的平移得到的.
![]() 若点
若点![]() 是点
是点![]() 通过
通过![]() 中的平移变换得到的,求
中的平移变换得到的,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com