
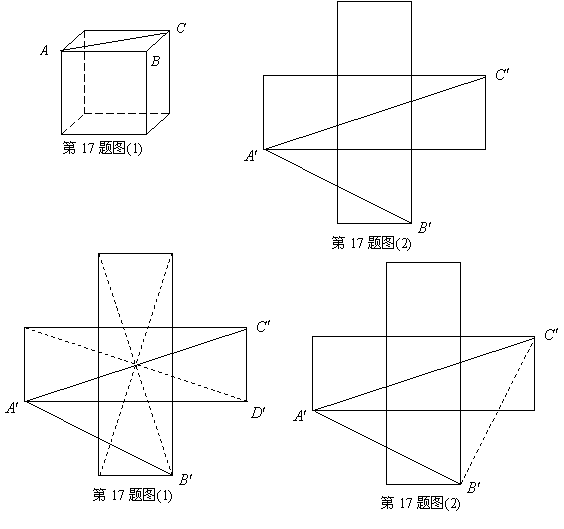
如图(1)所示为一上面无盖的正方体纸盒,现将其剪开展成平面图,如图(2)所示.已知展开图中每个正方形的边长为1.
(1)求在该展开图中可画出最长线段的长度?这样的线段可画几条?
(2)试比较立体图中 与平面展开图中
与平面展开图中 的大小关系?
的大小关系?
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
截止2008年6月1日12时,我国各级政府共投入四川汶川救灾资金达22609000000元,这项资金用科学记数法表示为( )
A、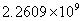 元;
元;  B、
B、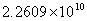 元;
元;
C、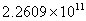 元 ; D、
元 ; D、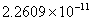 元
元
查看答案和解析>>
科目:初中数学 来源: 题型:
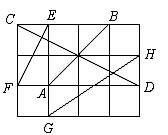
如图,在单位正方形组成的网格图中标有AB、CD、EF、GH四条线段,其中能构成一个直角三角形三边的线段是( )
A. CD、EF、GH B. AB、EF、GH
C. AB、CD、GH D. AB、CD、EF
查看答案和解析>>
科目:初中数学 来源: 题型:
观察下列各式,你有什么发现?
32=4+5,52=12+13,72=24+25,92=40+41…
这到底是巧合,还是有什么规律蕴涵其中呢?请你结合有关知识进行研究.如果132=b+c,则b、c的值可能是多少
查看答案和解析>>
科目:初中数学 来源: 题型:
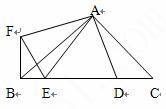
如图,在RtΔABC中,AB=AC,D,E是斜边BC上两点,且∠DAE=45º,将ΔADC绕点A顺时针旋转90º后,得到ΔAFB,连结EF.则∠EAF=____.
查看答案和解析>>
科目:初中数学 来源: 题型:
为确保信息安全,信息需加密传输,发送方由明文→密文(加密);接收方由密文→明文(解密).已知加密规则为:明文a,b,c,d对应密文 a+2b,2b+c,2c+3d,4d.例如:明文1,2,3,4对 应的密文5,7,18,16.当接收方收到密文14,9,23,28时,则解密得到的明文为( )
应的密文5,7,18,16.当接收方收到密文14,9,23,28时,则解密得到的明文为( )
(A) 4,6,1,7 (B) 4,1,6,7
(B) 4,1,6,7
(C)6,4,1,7 (D)1,6,4,7
查看答案和解析>>
科目:初中数学 来源: 题型:
某县社会主义新农村建设办公室,为了解决该县甲、乙两村和一所中学长期存在的饮水困难问题,想在这三个地方的其中一处建一所供水站,由供水站直接铺设管道到另外两处。
如图,甲、乙两村坐落在夹角为30°的两条公路的AB段和CD段(村子和公路的宽均不计),点M表示这所中学。点B在点M的北偏西30°的3km处,点A在点M的正西方向,点D在点M的南偏西60°的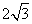 km处。
km处。
为使供水站铺设到另两处的管道长度之和最短,现有如下三种方案:
方案一:供水站建在点M处,请你求出铺设到甲村某处和乙村某处的管道长度之和的最小值;
方案二:供水站建在乙村(线段CD某处),甲村要求管道铺设到A处,请你在图①中,画出铺设到点A和点M处的管道长度之和最小的线路图,并求其最小值;
方案三:供水站建在甲村(线段AB某处),请你在图②中,画出铺设到乙村某处和点M处的管道长度之和最小的线路图,并求其最小值。
 综上,你认为把供水站建在何处,所需铺设的管道最短?
综上,你认为把供水站建在何处,所需铺设的管道最短?
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com