
 端午节是我国四大传统文化节日之一,为每年的农历五月初五,自古以来端午节便有划龙舟及食粽等习俗.重庆某大型超市为了了解市民对“蛋黄粽”的喜好程度,特意在三峡广场做了试吃及问卷调查活动,将市民对“蛋黄粽”的喜好程度分为“A非常喜欢”、“B比较喜欢”、“C感觉一般”、“D不太喜欢”四个等级,并将四个等级分别计分为:A等级10分,B等级7分,C等级5分,D等级2分,根据调查结果绘制出如图所示的条形统计图,请问“蛋黄粽”的平均分是7分.
端午节是我国四大传统文化节日之一,为每年的农历五月初五,自古以来端午节便有划龙舟及食粽等习俗.重庆某大型超市为了了解市民对“蛋黄粽”的喜好程度,特意在三峡广场做了试吃及问卷调查活动,将市民对“蛋黄粽”的喜好程度分为“A非常喜欢”、“B比较喜欢”、“C感觉一般”、“D不太喜欢”四个等级,并将四个等级分别计分为:A等级10分,B等级7分,C等级5分,D等级2分,根据调查结果绘制出如图所示的条形统计图,请问“蛋黄粽”的平均分是7分.  百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | .①③④ | B. | .②③ | C. | .①②③④ | D. | .①②③ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
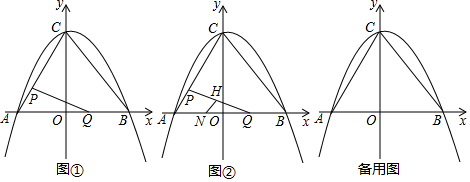
 如图,在平面直角坐标系中,点O为坐标原点,点A在第一象限且在直线y=$\frac{4}{3}$x上,点B为线段OA的中点,过点A作y轴的垂线,点D是线段AC的延长线上的一点,连接BD.若∠OBD=3∠D,且CD=5,则直线BD的解析式为y=-$\frac{1}{2}$x+$\frac{11}{2}$.
如图,在平面直角坐标系中,点O为坐标原点,点A在第一象限且在直线y=$\frac{4}{3}$x上,点B为线段OA的中点,过点A作y轴的垂线,点D是线段AC的延长线上的一点,连接BD.若∠OBD=3∠D,且CD=5,则直线BD的解析式为y=-$\frac{1}{2}$x+$\frac{11}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
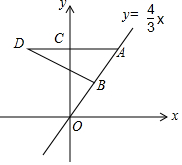
 在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示,△ABC先向右平移5格,再向上平移3格,得到△A1B1C1.
在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示,△ABC先向右平移5格,再向上平移3格,得到△A1B1C1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
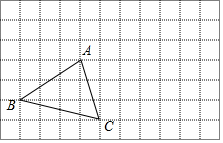
 某厂举办职工技能大赛,甲、乙两个车间各派5名选手参加,他们的分数见图表:
某厂举办职工技能大赛,甲、乙两个车间各派5名选手参加,他们的分数见图表:| 1号 | 2号 | 3号 | 4号 | 5号 | |
| 甲车间 | 75 | 80 | 85 | 85 | 100 |
| 乙车间 | 70 | 100 | x | 75 | 80 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com