
 如图是一张长方形纸片ABCD,若AB=8,AD=6,E为AB上的一点,AE=5,现要剪下一张等腰三角形纸片(△AEP),使点P落在长方形ABCD的某一条边上,则等腰三角形AEP的底边长是5或4$\sqrt{5}$或5$\sqrt{2}$.
如图是一张长方形纸片ABCD,若AB=8,AD=6,E为AB上的一点,AE=5,现要剪下一张等腰三角形纸片(△AEP),使点P落在长方形ABCD的某一条边上,则等腰三角形AEP的底边长是5或4$\sqrt{5}$或5$\sqrt{2}$. 分析 分情况讨论:①当AP=AE=5时,则△AEP是等腰直角三角形,得出底边PE=$\sqrt{2}$AE=5 $\sqrt{2}$即可;
②当PE=AE=5时,求出BE,由勾股定理求出PB,再由勾股定理求出等边AP即可;
③当PA=PE时,底边AE=5;即可得出结论.
解答 解:解:如图所示: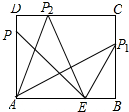
①当AP=AE=5时,
∵∠BAD=90°,
∴△AEP是等腰直角三角形,
∴底边PE=$\sqrt{2}$AE=5 $\sqrt{2}$;
②当PE=AE=5时,
∵BE=AB-AE=8-5=3,∠B=90°,
∴PB=$\sqrt{P{E}^{2}-B{E}^{2}}$=4,
∴底边AP=$\sqrt{A{B}^{2}+P{B}^{2}}$=$\sqrt{{8}^{2}+{4}^{2}}$=4 $\sqrt{5}$;
③当PA=PE时,底边AE=5;
综上所述:等腰三角形AEP的对边长为5 $\sqrt{2}$或4 $\sqrt{5}$或5;
故答案为5或4$\sqrt{5}$或5$\sqrt{2}$.
点评 本题考查了矩形的性质、等腰三角形的判定、勾股定理;熟练掌握矩形的性质和等腰三角形的判定,进行分类讨论是解决问题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 7×10-7mm2 | B. | 0.7×10-6mm2 | C. | 7×10-8mm2 | D. | 70×10-8mm2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
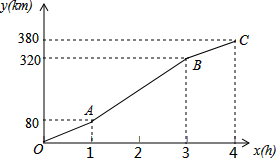 暑假期间,小刚一家乘车去离家380km的某景区旅游,他们离家的距离y(km)与汽车行驶时间x(h)之间的函数图象如图所示.
暑假期间,小刚一家乘车去离家380km的某景区旅游,他们离家的距离y(km)与汽车行驶时间x(h)之间的函数图象如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com