

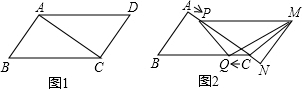
分析 (1)如图1,过E作EM⊥AD于M,由四边形ABCD是菱形,得到AD=CD,∠ADE=∠CDE,通过△DME≌△DHE,根据全等三角形的性质得到EM=EH,DM=DH,等量代换得到AM=CH,根据勾股定理即可得到结论;
(2)如图2,根据菱形的性质得到∠BDC=∠BDA=30°,DA=DC,在CH上截取HG,使HG=EH,推出△DEG是等边三角形,由等边三角形的性质得到∠EDG=60°,推出△DAE≌△DCG,根据全等三角形的性质即可得到结论.
解答  解:(1)EH2+CH2=AE2,
解:(1)EH2+CH2=AE2,
如图1,过E作EM⊥AD于M,
∵四边形ABCD是菱形,
∴AD=CD,∠ADE=∠CDE,
∵EH⊥CD,
∴∠DME=∠DHE=90°,
在△DME与△DHE中,
$\left\{\begin{array}{l}{∠DME=∠DHE}\\{∠MDE=∠HDE}\\{DE=DE}\end{array}\right.$,
∴△DME≌△DHE,
∴EM=EH,DM=DH,
∴AM=CH,
在Rt△AME中,AE2=AM2+EM2,
∴AE2=EH2+CH2;
(2)如图2,CH=AE+EH,
理由:∵菱形ABCD,∠ADC=60°,
∴∠BDC=∠BDA=30°,DA=DC,
∵EH⊥CD,
∴∠DEH=60°,
在CH上截取HG,使HG=EH,
∵DH⊥EG,∴ED=DG,
又∵∠DEG=60°,
∴△DEG是等边三角形,
∴∠EDG=60°,
∵∠EDG=∠ADC=60°,
∴∠EDG-∠ADG=∠ADC-∠ADG,
∴∠ADE=∠CDG,
在△DAE与△DCG中,$\left\{\begin{array}{l}{DA=DC}\\{∠ADE=∠CDG}\\{DE=DG}\end{array}\right.$,
∴△DAE≌△DCG,
∴AE=GC,
∵CH=CG+GH,
∴CH=AE+EH.
点评 本题考查了全等三角形的判定和性质,菱形的性质,旋转的性质,等边三角形的判定和性质,正确的作出辅助线是解题的关键.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在边长为2的正方形ABCD中,G是AD延长线上的一点,且DG=AD,动点M从A点出发,以每秒1个单位的速度沿着A→C→G的路线向G点匀速运动(M不与A,G重合),设运动时间为t秒,连接BM并延长交AG于N.
如图,在边长为2的正方形ABCD中,G是AD延长线上的一点,且DG=AD,动点M从A点出发,以每秒1个单位的速度沿着A→C→G的路线向G点匀速运动(M不与A,G重合),设运动时间为t秒,连接BM并延长交AG于N.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
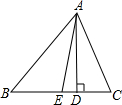 如图所示,△ABC中,AD⊥BC,AE平分∠BAC.
如图所示,△ABC中,AD⊥BC,AE平分∠BAC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 求不等式组$\left\{\begin{array}{l}{3x+3>5(x-1)①}\\{\frac{2x-2}{3}-1≤\frac{3x}{2}②}\end{array}\right.$的解集,并把它们的解集在数轴上表示出来.
求不等式组$\left\{\begin{array}{l}{3x+3>5(x-1)①}\\{\frac{2x-2}{3}-1≤\frac{3x}{2}②}\end{array}\right.$的解集,并把它们的解集在数轴上表示出来.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com