
【题目】解下列不等式(组),并把解集在数轴上表示出来:
(1)![]()
(2)![]()
【答案】(1)x>-1;(2)-1≤x<3.
【解析】
(1)先去分母得到6-2(2-x)<3(x+1),再去括号、移项、合并得到-x<1,然后把x的系数化为1即可得到不等式的解集,再利用数轴表示解集;
(2)分别解两个不等式得到x<3和x≥-1,然后根据大于小的小于大的取中间确定不等式组的解集,再利用数轴表示解集;
解:(1)去分母,得:6-2(2-x)<3(x+1),
去括号,得:6-4+2x<3x+3,
移项,得:2x-3x<3+4-6,
合并同类项,得:-x<1,
系数化为1,得:x>-1,
这个不等式的解集在数轴上表示为:
 ;
;
(2)![]()
解不等式①,得:x<3,
解不等式②,得:x≥-1,
所以原不等式组的解集为:-1≤x<3,
这个不等式的解集在数轴上表示为:

故答案为:(1)x>-1;(2)-1≤x<3.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,点C、D在⊙O上,点E在⊙O外,∠EAC=∠D=60°.
(1)求证:AE是⊙O的切线;
(2)当BC=4时求劣弧AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由于雾霾天气持续笼罩某地区,口罩市场出现热卖.某商店用8000元购进甲、乙两种口罩,销售完后共获利2800元,其进价和售价如下表:
甲种口罩 | 乙种口罩 | |
进价(元/袋) | 20 | 25 |
售价(元/袋) | 26 | 35 |
(1)求该商店购进甲、乙两种口罩各多少袋?
(2)该商店第二次仍以原价购进甲、乙两种口罩,购进乙种口罩袋数不变,而购进甲种口罩袋数是第一次的2倍,甲种口罩按原售价出售,而乙种口罩让利销售.若两种口罩销售完毕,要使第二次销售活动获利不少于3680元,则乙种口罩最低售价为每袋多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
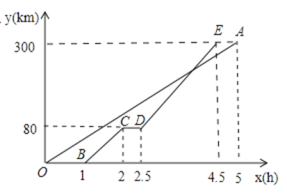
【题目】甲、乙两地相距300km,一辆货车和一辆轿车先后从甲地出发驶向乙地。如图,线段OA表示货车离甲地的距离![]() (km)与时间
(km)与时间![]() (h)之间的函数关系,折线BCDE变式轿车离甲地的距离
(h)之间的函数关系,折线BCDE变式轿车离甲地的距离![]() (km)与时间
(km)与时间![]() (h)之间的函数关系。根据图像,解答下列问题:
(h)之间的函数关系。根据图像,解答下列问题:
(1)线段CD表示轿车在途中停留了 h.
(2)求线段DE对应的函数关系式(2.5≤x≤4.5).
(3)求轿车从甲地出发后经过多长时间追上货车.
查看答案和解析>>
科目:初中数学 来源: 题型:
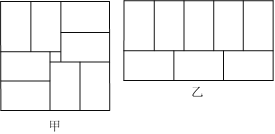
【题目】小明用8个一样大的小长方形(长![]() ,宽为
,宽为![]() )拼图,拼出了如图甲、乙的两种图案:图甲是一个正方形,图案乙是一个大的长方形;图案甲的中间留下了边长是2 cm的正方形小洞.
)拼图,拼出了如图甲、乙的两种图案:图甲是一个正方形,图案乙是一个大的长方形;图案甲的中间留下了边长是2 cm的正方形小洞.
(1)求小长方形长、宽.
(2)求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
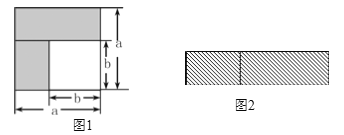
【题目】乘法公式的探究及应用.
(1)如图1,可以求出阴影部分的面积是 (写成两数平方差的形式);
(2)如图2,若将阴影部分裁剪下来,重新拼成一个矩形,它的宽是 ,长是 ,面积是 (写成多项式乘法的形式);
(3)比较图1、图2两图的阴影部分面积,可以得到乘法公式 (用式子表达);
(4)运用你所得到的公式,计算下列各题:
①(2m+n-p)(2m-n+p);②10.3×9.7.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD的长和宽分别为16cm和12cm,连接其对边中点,得到四个矩形,顺次连接矩形AEFG各边中点,得到菱形l1;连接矩形FMCH对边中点,又得到四个矩形,顺次连接矩形FNPQ各边中点,得到菱形l2;…如此操作下去,则l4的面积是cm2 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com