
 )在x轴上运动,过A作直线MC的垂线交y轴于点N.
)在x轴上运动,过A作直线MC的垂线交y轴于点N.
|
|
|
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
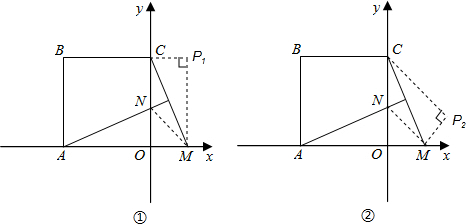


科目:初中数学 来源: 题型:
20
| ||
| 3 |
| 2 |
| 3 |
| 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:
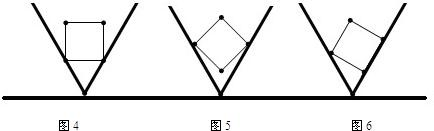
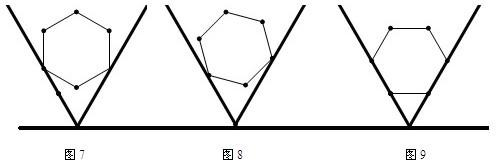
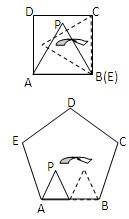 16、如图,已知正方形ABCD的边长AB=1,正△PAE的边长AE=1,开始时正△PAE与正方形ABCD边AB重合,顶点P在正方形内,将正△PAE在正方形内按如图所示的方式,沿着正方形的边AB、BC、CD、DA、AB、BC…连续地翻转
16、如图,已知正方形ABCD的边长AB=1,正△PAE的边长AE=1,开始时正△PAE与正方形ABCD边AB重合,顶点P在正方形内,将正△PAE在正方形内按如图所示的方式,沿着正方形的边AB、BC、CD、DA、AB、BC…连续地翻转查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
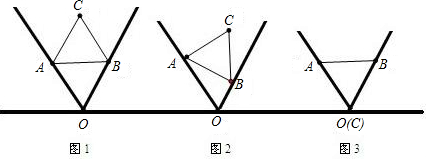
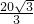 ,请通过计算或证明说明,三种放法中,哪一种放法最稳定?
,请通过计算或证明说明,三种放法中,哪一种放法最稳定?
 ≈1.4;
≈1.4; ≈1.7;
≈1.7; ≈2.4)
≈2.4)

查看答案和解析>>
科目:初中数学 来源:2010年数学参赛试卷2010.3吴(解析版) 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com