
【题目】为了打造区域中心城市,实现跨越式发展,我市新区建设正按投资计划有序推进.新区建设工程部,因道路建设需要开挖土石方,计划每小时挖掘土石方540m3,现决定向某大型机械租赁公司租用甲、乙两种型号的挖掘机来完成这项工作,租赁公司提供的挖掘机有关信息如表:

(1)若租用甲、乙两种型号的挖掘机共8台,恰好完成每小时的挖掘量,则甲、乙两种型号的挖掘机各需多少台?
(2)如果每小时支付的租金不超过850元,又恰好完成每小时的挖掘量,那么共有几种不同的租用方案?
【答案】(1)5台、3台(2)有一种租车方案,即租用1辆甲型挖掘机和6辆乙型挖掘机
【解析】试题分析:(1)设甲、乙两种型号的挖掘机各需x台、y台.等量关系:甲、乙两种型号的挖掘机共8台;每小时挖掘土石方540m3;
(2)设租用m辆甲型挖掘机,n辆乙型挖掘机,根据题意列出二元一次方程,求出其正整数解;然后分别计算支付租金,选择符合要求的租用方案.
试题解析:(1)设甲、乙两种型号的挖掘机各需x台、y台.
依题意得: ![]()
解得![]() .
.
答:甲、乙两种型号的挖掘机各需5台、3台;
(2)设租用![]() 台甲型挖掘机,
台甲型挖掘机, ![]() 台乙型挖掘机.
台乙型挖掘机.
依题意得: ![]() (
(![]() ,
, ![]() 均为自然数),
均为自然数),
∴![]()
∴方程的解为![]() .
.
当m=9,n=0时,支付租金:100×9+120×0=900元>850元,超出限额;
当m=5,n=3时,支付租金:100×5+120×3=860元>850元,超出限额;
当m=1,n=6时,支付租金:100×1+120×6=820元,符合要求.
答:有一种租车方案,即租用1辆甲型挖掘机和6辆乙型挖掘机.


 星级口算天天练系列答案
星级口算天天练系列答案科目:初中数学 来源: 题型:
【题目】在下列网格图中,每个小正方形的边长均为1个单位.在Rt△ABC中,∠C=90°,AC=3,BC=4.

(1)试在图中做出△ABC以A为旋转中心,沿顺时针方向旋转90°后的图形△AB1C1;
(2)若点B的坐标为(﹣3,5),试在图中画出直角坐标系,并标出A、C两点的坐标;
(3)根据(2)的坐标系作出与△ABC关于原点对称的图形△A2B2C2,并标出B2、C2两点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水库的水位在5小时内持续上涨,初始的水位高度为6米,水位以每小时0.3米的速度匀速上升,则水库的水位高度y米与时间x小时(0≦x≦5)的函数关系式为___
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB,CD是⊙O的直径,点E在AB延长线上,FE⊥AB,BE=EF=2,FE的延长线交CD延长线于点G,DG=GE=3,连接FD.
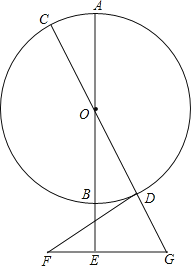
(1)求⊙O的半径;
(2)求证:DF是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面推理过程:
如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD.理由如下:
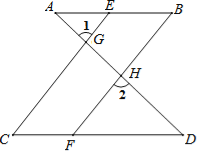
∵∠1=∠2(已知),
且∠1=∠CGD( ),
∴∠2=∠CGD(等量代换).
∴CE∥BF( ).
∴∠ =∠C( ).
又∵∠B=∠C(已知),
∴∠ =∠B(等量代换).
∴AB∥CD( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某中学举行“中国梦校园好声音”歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.
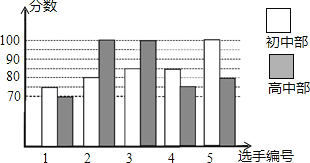
(1)根据图示填写下表;
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.
平均数(分) | 中位数(分) | 众数(分) | |
初中部 |
| 85 |
|
高中部 | 85 |
| 100 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两台机器共加工一批零件,在加工过程中两台机器均改变了一次工作效率.从工作开始到加工完这批零件两台机器恰好同时工作6小时.甲、乙两台机器各自加工的零件个数y(个)与加工时间x(时)之间的函数图象分别为折线OA﹣AB与折线OC﹣CD.如图所示.
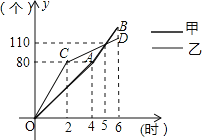
(1)甲机器改变工作效率前每小时加工零件 个.
(2)求乙机器改变工作效率后y与x之间的函数关系式,并求出自变量x的取值范围.
(3)求这批零件的总个数.
(4)直接写出当甲、乙两台机器所加工零件数相差10个时,x的值为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com