
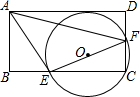
 如图,矩形ABCD中,E为BC上一点,F为CD上一点,已知∠AEF=90°,$\frac{AE}{EF}$=$\frac{3}{4}$,△ECF的外接圆与AD相切,则tan∠DAF=$\frac{16}{63}$.
如图,矩形ABCD中,E为BC上一点,F为CD上一点,已知∠AEF=90°,$\frac{AE}{EF}$=$\frac{3}{4}$,△ECF的外接圆与AD相切,则tan∠DAF=$\frac{16}{63}$. 分析 设⊙O与直线AD相切于点M,连接MO,延长MO交BC于点N,设AE=AM=3k,AB=3a,由△ABE∽△ECF求出EC,在RT△ABE中,利用勾股定理求出a、k之间的关系,利用DM2=DF•DC求出DF,根据tan∠DAF=$\frac{DF}{AD}$即可解决问题.
解答 解:设⊙O与直线AD相切于点M,连接MO,延长MO交BC于点N,
设AE=AM=3k,AB=3a,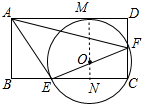 ∵∠AEF=90°,
∵∠AEF=90°,
∴∠AEB+∠FEC=90°,∠FEC+∠EFC=90°,
∴∠AEB=∠EFC,
∵∠C=∠B=90°,
∴△ABE∽△ECF,
∴$\frac{AB}{EC}=\frac{AE}{EF}=\frac{3}{4}$,
∴EC=4a,
∵OM⊥AD.AD∥BC,
∴ON⊥BC,
∴NE=NC=DM=2a,
∴BE=3k+2a-4a=3k-2a,
在RT△ABE中,∵AE2=AB2+BE2,
∴9k2=9a2+(3k-2a)2,
∴k=$\frac{13}{12}$a,
∴AM=$\frac{13}{4}$a,
∵DM2=DF•DC,
∴DF=$\frac{4}{3}$a,
∴tan∠ADF=$\frac{DF}{AD}$=$\frac{\frac{4}{3}a}{\frac{21}{4}a}$=$\frac{16}{63}$.
故答案为$\frac{16}{63}$.
点评 本题考查矩形的性质、切线长定理、切割线定理、勾股定理等知识,解题的关键是设两个参数,利用勾股定理推出两个参数之间的关系,题目比较难,属于中考填空题中的压轴题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
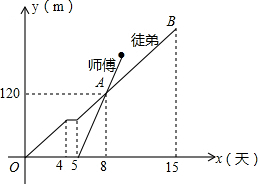 为了检修自来水管道,由师徒两人完成,两人从管道两端开始检修,已知徒弟先修了4天后,休息了1天,接着师徒两人合做了5天,师傅被安排做其他工作,余下由徒弟单独检修完,如图是师傅和徒弟修管道的长度与工作时间的函数图象,请根据图象提供的信心解答下列问题.
为了检修自来水管道,由师徒两人完成,两人从管道两端开始检修,已知徒弟先修了4天后,休息了1天,接着师徒两人合做了5天,师傅被安排做其他工作,余下由徒弟单独检修完,如图是师傅和徒弟修管道的长度与工作时间的函数图象,请根据图象提供的信心解答下列问题.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com