
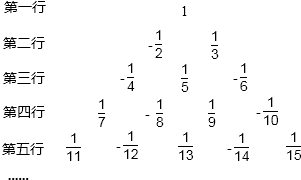
分析 当分母是奇数时,为正号.当分母是偶数时,符号是负号.所有的分子都是1.分母是从1开始连续的整数,第n行末尾的分母即是1+2+3+…+n=$\frac{1}{2}$n(n+1).根据这一规律,分析得出答案即可.
解答 解:∵分母是从1开始连续的整数,第n行末尾的分母即是1+2+3+…+n=$\frac{1}{2}$n(n+1),
∴$\frac{1}{2}$×63×64=2016,$\frac{1}{2}$×62×63=1953,
∴-$\frac{1}{2006}$在第63行,第2006-1953=53个.
故答案为:63,53.
点评 此题考查数字的变化规律,找出数字的排列规律,得出数字之间的运算规律,利用规律解决问题.


科目:初中数学 来源: 题型:填空题
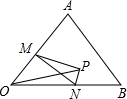 如图,在△AOB内有一定点P,OP=3,∠AOB=45°,点M,N分别为AO,BO上的点,那么△PMN的周长的最小值是3$\sqrt{2}$,此时,∠MPN的度数是90°.
如图,在△AOB内有一定点P,OP=3,∠AOB=45°,点M,N分别为AO,BO上的点,那么△PMN的周长的最小值是3$\sqrt{2}$,此时,∠MPN的度数是90°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
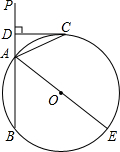 如图,AE是⊙O的直径,CD是⊙O的切线,切点为C,直线BP交⊙O于A、B两点且垂直于CD,垂足为点D,
如图,AE是⊙O的直径,CD是⊙O的切线,切点为C,直线BP交⊙O于A、B两点且垂直于CD,垂足为点D,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com