
【题目】如图,二次函数![]() (其中
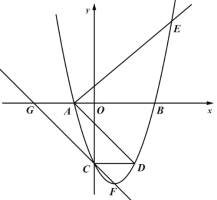
(其中![]() )的图象与x轴分别交于点A、B(点A位于B的左侧),与y轴交于点C,过点C作x轴的平行线CD交二次函数图像于点D.
)的图象与x轴分别交于点A、B(点A位于B的左侧),与y轴交于点C,过点C作x轴的平行线CD交二次函数图像于点D.
(1)当m2时,求A、B两点的坐标;
(2)过点A作射线AE交二次函数的图像于点E,使得BAEDAB.求点E的坐标(用含m的式子表示);
(3)在第(2)问的条件下,二次函数![]() 的顶点为F,过点C、F作直线与x轴于点G,试求出GF、AD、AE的长度为三边长的三角形的面积(用含m的式子表示).
的顶点为F,过点C、F作直线与x轴于点G,试求出GF、AD、AE的长度为三边长的三角形的面积(用含m的式子表示).
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)求图象与x轴交点,即函数y值为零,解一元二次方程即可;
(2)过![]() 作
作![]() 轴,过
轴,过![]() 作
作![]() 轴,先求出D点坐标为
轴,先求出D点坐标为![]() ,设E点为
,设E点为![]() ,即可列等式求m的值得E点坐标;
,即可列等式求m的值得E点坐标;
(3)由直线![]() 的方程:
的方程:![]() ,得G点坐标,再用m的表达式分别表达GF、AD、AE即可.
,得G点坐标,再用m的表达式分别表达GF、AD、AE即可.
(1) 当![]() 时,
时,![]() ,
,
∵![]() 图象与x轴分别交于点A、B
图象与x轴分别交于点A、B
∴![]() 时,
时,![]()
∴![]() ,
,![]()
(2)∵![]() ,
,![]() 轴
轴
∴![]()
过![]() 作
作![]() 轴,过
轴,过![]() 作
作![]() 轴
轴
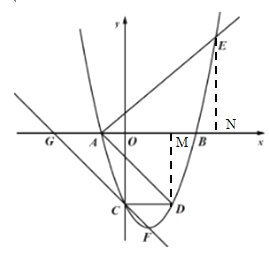
∵![]()
∴![]()
设E![]()
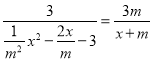
∴![]()
![]()
(3)以GF、BD、BE的长度为三边长的三角形是直角三角形.理由如下:
二次函数![]() 的顶点为F,则F的坐标为(m,4),过点F作FH⊥x轴于点H.
的顶点为F,则F的坐标为(m,4),过点F作FH⊥x轴于点H.
∵tan∠CGO=![]() ,tan∠FGH=
,tan∠FGH=![]() ,
,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∵OC=3,HF=4,OH=m,
∴![]() ,
,
∴OG=3m.
∴![]()
![]()
![]()
![]() ,
,
∴![]()
∴![]() 、
、![]() 、
、![]() 能构成直角三角形面积是
能构成直角三角形面积是![]()
所以![]() 、
、![]() 、
、![]() 能构成直角三角形面积是
能构成直角三角形面积是![]()


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
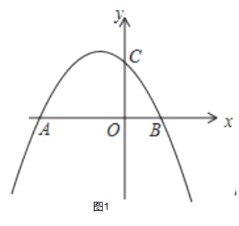
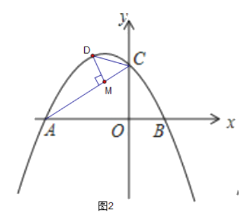
【题目】如图1,二次函数![]() 的图象与x轴交于点A、B,与y轴交于点C,点A的坐标为(﹣4,0)
的图象与x轴交于点A、B,与y轴交于点C,点A的坐标为(﹣4,0)
(1)b= ,点B的坐标是 ;
(2)连接AC、BC,判断∠CAB和∠CBA的数量关系,并说明理由
(3)如图2,点D是抛物线上第二象限内的一动点,过点D作DM⊥AC于点M,是否存在点D,使得△CDM中的某个角恰好等于∠BAC的2倍?若存在,写出点D的横坐标;若不存在,请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周末上午小明和大强分别从家出发,相约一起去体育馆打球,小明比大强先出发![]() ,大强出发
,大强出发![]() 后与小明相遇.小明的行进速度为
后与小明相遇.小明的行进速度为![]() ,设小明、大强两人相距
,设小明、大强两人相距![]() 与小明行进的时间
与小明行进的时间![]() 之间的函数关系如图所示:
之间的函数关系如图所示:
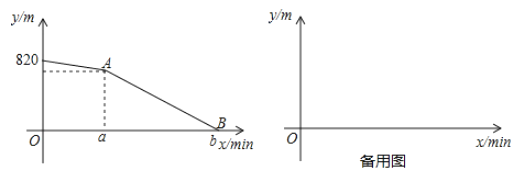
(1)填空:![]() ,小明和大强家相距
,小明和大强家相距 ![]() :
:
(2)求线段![]() 对应的函数表达式,并直接写出自变量
对应的函数表达式,并直接写出自变量![]() 的取值范围;
的取值范围;
(3)设大强离家的距离为![]() ,小明行进的时间
,小明行进的时间![]() ,求
,求![]() 与
与![]() 的函数关系式,并画出函数的图象.
的函数关系式,并画出函数的图象.
查看答案和解析>>
科目:初中数学 来源: 题型:
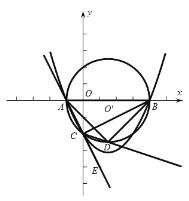
【题目】已知:二次函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() 两点,其中点
两点,其中点![]() ,与
,与![]() 轴负半轴交于点
轴负半轴交于点![]() ,起对称轴是直线
,起对称轴是直线![]() .
.
(1)求二次函数![]() 的解析式;
的解析式;
(2)圆![]() 经过点
经过点![]() 的外接圆,点
的外接圆,点![]() 是
是![]() 延长线上一点,
延长线上一点,![]() 的平分线交圆
的平分线交圆![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() ,求
,求![]() 的面积;
的面积;
(3)在(2)的条件下,二次函数![]() 的图象上是否存在点
的图象上是否存在点![]() ,使得
,使得![]() ?如果存在,请求出所有符合条件的
?如果存在,请求出所有符合条件的![]() 点坐标;如果不存在,请说明理由.
点坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y ax2 2ax 3a2 3(其中x是自变量),当x 2时,y随x的增大而增大,且3 x 0时,y的最大值为9,则a的值为( ).
A.1或![]() B.
B.![]() 或
或![]() C.
C.![]() D.1
D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电子产品销售公司专门销售某种品牌的电子产品.该公司给职工的工资由两部分组成:一是基本保障工资,二是销售奖励工资(销售奖励工资=销售每件产品的奖励金额×销售的件数).下表是小张、小李两位职工今年11月份的工资情况信息:
职工 | 小张 | 小李 |
月销售件数(件) | 200 | 180 |
月工资(元) | 5000 | 4700 |
(1)该公司职工的月基本保障工资和销售每件产品的奖励金额各是多少元?
(2)该公司职工小王计划今年12月份获得不少于6000元,那么小王12月份至少应销售多少件产品?
查看答案和解析>>
科目:初中数学 来源: 题型:
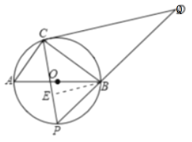
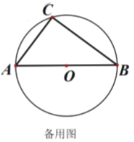
【题目】如图,直径![]() 把圆
把圆![]() 分为两个半圆,一个半圆弧上有一定点
分为两个半圆,一个半圆弧上有一定点![]() ,另一半圆弧上有一动点
,另一半圆弧上有一动点![]() .过
.过![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.
(1)求证:![]()
(2)若![]() ,
,![]()
①当点![]() 运动到半圆弧
运动到半圆弧![]() 中点时,求
中点时,求![]() 边
边![]() 上的高;
上的高;
②当点![]() 运动到什么位置时,
运动到什么位置时,![]() 的面积最大?并求这个最大面积
的面积最大?并求这个最大面积![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于实数a,b,我们可以用![]() 表示a,b两数中较大的数,例如
表示a,b两数中较大的数,例如![]() ,
,![]() .类似的若函数y1、y2都是x的函数,则y=min{y1,y2}表示函数y1和y2的取小函数.
.类似的若函数y1、y2都是x的函数,则y=min{y1,y2}表示函数y1和y2的取小函数.
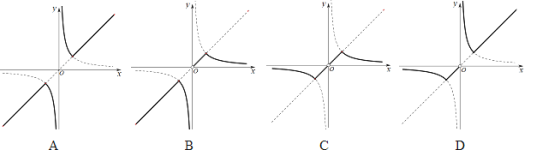
(1)设![]() ,
,![]() ,则函数
,则函数![]() 的图像应该是___________中的实线部分.
的图像应该是___________中的实线部分.
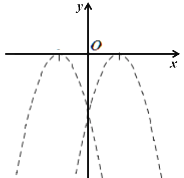
(2)请在下图中用粗实线描出函数![]() 的图像,观察图像可知当x的取值范围是_____________________时,y随x的增大而减小.
的图像,观察图像可知当x的取值范围是_____________________时,y随x的增大而减小.
(3)若关于x的方程![]() 有四个不相等的实数根,则t的取值范围是_____________________.
有四个不相等的实数根,则t的取值范围是_____________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
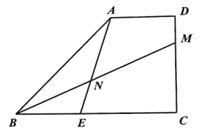
【题目】如图,在梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 在边
在边![]() 上,
上,![]() ,点
,点![]() 是射线
是射线![]() 上一个动点(不与点
上一个动点(不与点![]() 、
、![]() 重合),联结
重合),联结![]() 交射线
交射线![]() 于点
于点![]() ,设
,设![]() ,
,![]() .
.
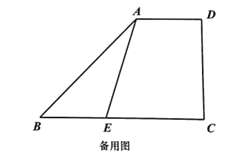
(1)求![]() 的长;
的长;
(2)当动点![]() 在线段
在线段![]() 上时,试求
上时,试求![]() 与
与![]() 之间的函数解析式,并写出函数的定义域;
之间的函数解析式,并写出函数的定义域;
(3)当动点![]() 运动时,直线
运动时,直线![]() 与直线
与直线![]() 的夹角等于
的夹角等于![]() ,请直接写出这时线段
,请直接写出这时线段![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com